На завтра нужно: доказать что существует натуральное число последние четыре цифры которого 1996 и кторое делится на 1997

👇

Увидеть ответ

Ответ:

Danfdffefd

30.04.2023

Покажи и покажи как есть

4,6(14 оценок)

Открыть все ответы

Ответ:

atlantisatlantp07ft0

30.04.2023

Пошаговое объяснение:

Пуговиц на красных пиджаках всего в 2 раза меньше , чем на зелёных,

так и количество пуговиц на одном красном пиджаке тоже меньше в 2 раза

4\2 = 2 раза.

А это значит , что красных и зеленых пиджаков поровну.

А в среднем на каждый пиджак приходится по 3 пуговицы( кр и зел)

А у синих пиджаков по 3 пуговицы, значит их столько же , сколько всего красных и зеленых.

А это значит , что половина всех пиджаков - синие

36 \ 2 = 18 синих ,

а остальные 18 - половина красные и половина зеленые

18 \ 2 = 9 красных и столько же зеленых \ 2

4,7(51 оценок)

Ответ:

DastyMilk

30.04.2023

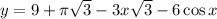
$y = 9 + \pi \sqrt{3} - 3x\sqrt{3} - 6\cos x$

$x \in \bigg[0; \ \dfrac{\pi}{2} \bigg]$

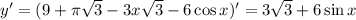
$y' = (9 + \pi \sqrt{3} - 3x\sqrt{3} - 6\cos x)' = 3\sqrt{3} + 6\sin x$

Найдем критические точки функции:

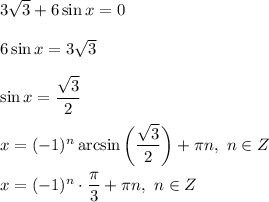
$3\sqrt{3} + 6\sin x = 0\\\\6\sin x = 3\sqrt{3}\\\\\sin x = \dfrac{\sqrt{3}}{2} \\\\x = (-1)^{n} \arcsin \bigg(\dfrac{\sqrt{3}}{2} \bigg) + \pi n, \ n \in Z\\\\x = (-1)^{n} \cdot \dfrac{\pi}{3} + \pi n, \ n \in Z$

Как видим, таких критических точек - множество. Определим некоторые из них, которые принадлежат отрезку $\bigg[0; \ \dfrac{\pi}{2} \bigg]$ . Для этого будем брать всевозможные целые значения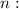

Пусть 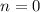n = 0 . Тогда $x = (-1)^{0} \cdot \dfrac{\pi}{3} + \pi \cdot 0 = \dfrac{\pi}{3} \in \bigg[0; \ \dfrac{\pi}{2} \bigg]$

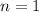Пусть n = 1 . Тогда $x = (-1)^{1} \cdot \dfrac{\pi}{3} + \pi \cdot 1 = -\dfrac{\pi}{3} + \pi = \dfrac{2\pi}{3} \notin \bigg[0; \ \dfrac{\pi}{2} \bigg]$

Только одно значение 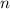, при котором данные критические точки входят в промежуток $\bigg[0; \ \dfrac{\pi}{2} \bigg]$

Итак, только на одном из трех вариантов: 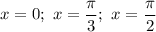$x = 0; \ x = \dfrac{\pi}{3}; \ x = \dfrac{\pi}{2}$ заданная функция может принимать наименьшее значение. Вычислим ее значение в этих трех точках, зная их абсциссы, и найдем наименьшее:

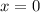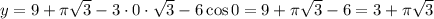
Если x = 0 , то $y = 9 + \pi \sqrt{3} - 3\cdot 0 \cdot \sqrt{3} - 6\cos 0 = 9 + \pi \sqrt{3} - 6 = 3 + \pi \sqrt{3}$

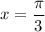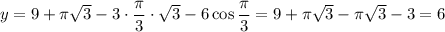
Если $x = \dfrac{\pi}{3}$ , то $y = 9 + \pi \sqrt{3} - 3\cdot \dfrac{\pi}{3} \cdot \sqrt{3} - 6\cos \dfrac{\pi}{3} = 9 + \pi \sqrt{3} - \pi \sqrt{3} - 3 = 6$

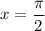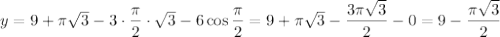
Если $x = \dfrac{\pi}{2}$ , то $y = 9 + \pi \sqrt{3} - 3\cdot \dfrac{\pi}{2} \cdot \sqrt{3} - 6\cos \dfrac{\pi}{2} = 9 + \pi \sqrt{3} - \dfrac{3\pi \sqrt{3}}{2} - 0 = 9 - \dfrac{\pi \sqrt{3}}{2}$

Для того чтобы определить наименьшее из трех, можно подставить приблизительное значение числа 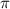$\pi$ , а именно 3,14. Видим, что наименьшим значением функции является точка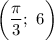 $\bigg(\dfrac{\pi}{3} ; \ 6 \bigg)$