Пошаговое объяснение:
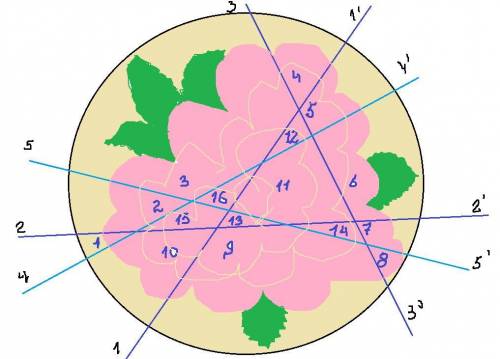
Если все 5 разрезов будут пересекаться в одной точке, то куски можно сделать ровные, каждый с равной частичкой розочки. но их будет всего 10, так как каждый из 5 разрезов делит торт пополам.
Если линии разреза не будут проходить через одну точку, а первые 3 образуют треугольник, обрамляющий часть розочки, то получится дополнительный кусок "с розочкой".
Если же каждая из двух других линий отсечет от треугольника еще по треугольному куску, один из которых они, пересекаясь между собой, разделят на треугольник и четырехугольник, то всего получится 16 кусков "с розочкой". Куски не равны по величине, некоторые совсем крошечные, на задача выполнена. Получено максимальное число кусков с частичкой розы. Главное, чтобы роза и торт были большими!
ответ: может повезти 16 детишкам.
Евклид и его “Начала”
В течение двух тысяч лет геометрию узнавали либо из “Начал” Евклида, либо из учебников, написанных на основе этой книги. Лишь профессиональные математики обращались к трудам других великих греческих геометров: Архимеда, Аполлония и геометров более позднего времени. Классическую геометрию стали называть евклидовой в отличие от появившихся в XIX в “неевклидовой геометрий”.
Об этом поразительном человеке история сохранила настолько мало сведений, что не редко высказываются сомнения в самом его существовании. Что же дошло до нас? Каталог греческих геометров Прокла Диадоха Византийского, жившего в V в н. э. , -первый серьёзный источник сведений о греческой геометрии. Из каталога следует, что Евклид был современником царя Птолемея I,который царствовал с 306-283г. до н. э.
Евклид должен быть старше Архимеда, который ссылался на “Начало”. До наших времён дошли сведения, что он преподавал в Александрии, столица Птолемея I, начинавший превращаться в один из центров научной жизни. Евклид был последователем древнегреческого философа Платона, и преподавал он, вероятно, четыре науки, которые, по мнению Платона, должны предшествовать занятиям философией: арифметику, геометрию, теорию гармонии, астрономию. Кроме “Начал” до нас дошли книги Евклида, посвящённые гармонии и астрономии.
Что касается места Евклида в науке, то оно определяется не столько собственными его научными исследованиями, сколько педагогическими заслугами. Евклиду приписывается несколько теорем и новых доказательств, но их значение не может быть сравнимо с достижениями великих греческих геометров: Фалеса и Пифагора (VI век до н. э.) , Евдокса и Теэтета (IV век до н. э.) . Величайшая заслуга Евклида в том, что он подвёл итог построению геометрии и придал изложению столь совершенную форму, что на 2000 лет “Начала” стали энциклопедией геометрии.
Евклид с величайшим искусством расположил материал по 13 книгам так, чтобы трудности не возникали преждевременно. Позже греческие математики включили в “Начало” ещё две книги-XIV- и XV-ю, написанные другими авторами.
Первая книга Евклида начинается с 23”определений”, среди них такие: точка есть то, что не имеет частей; линяя есть длина без ширины; линия ограничена точками; прямая есть линия, одинакова расположенная относительно всех своих точек; наконец, две прямые, лежащие в одной плоскости, называются параллельными, если они, сколь угодно продолжены, не встречаются. Это скорее наглядные представления об основных объектах и слово “определение” в современном понимании не точно передаёт смысл греческого слова “хорой”, которым пользовался Евклид.
В книге I рассматриваются основные свойства треугольников, прямоугольников, параллелограммов, сравниваются их площади. Здесь появляется теорема о сумме углов треугольника. Затем следует пять геометрических постулатов: через две точки можно провести одну прямую; каждая прямая может быть сколь угодно продолжена ; данным радиусом из данной точки можно провести окружность; все прямые углы равны; если две прямые проведены к третьей под углами, составляющими в сумме меньше двух прямых, то они встречаются с той же стороны от этой прямой. Все эти постулаты, кроме одного, вошли в современные курсы основной геометрии. За постулатами приводятся общие предположения, или аксиомы, - 8 общематематических утверждений о равенствах и неравенствах. Книга заканчивается теоремой Пифагора.
В книге II излагается геометрическая алгебра, с геометрических чертежей даются решения задач, сводящихся к квадратным уравнениям. Алгебраической символики тогда не существовало.