5.Угловой коэффициент = значению производной в точке -3
производная равна х²-4х
y'(-3)=9+12=21
6. производная равна 6х²+18х=6х*(х+3)=0
___-30
+ - +
на промежутках (-∞;-3] и [0;+∞) функция возрастает, а на [-34;0] убывает. х=-3 - точка максимума, х=0- точка минимума.
7. 0=(х-3)²⇒х=2; х=3- пределы интегрирования.
найдем определенный интеграл от 2 до 3 от функции (х²-6х+9-0)
В х³/3-3х²+9х подставим по формуле Ньютона - Лейбница пределы интегрирования, найдем площадь. 9-27+27-(8/3-12+18)=3/(8/3)=
1/3/ед. кв./
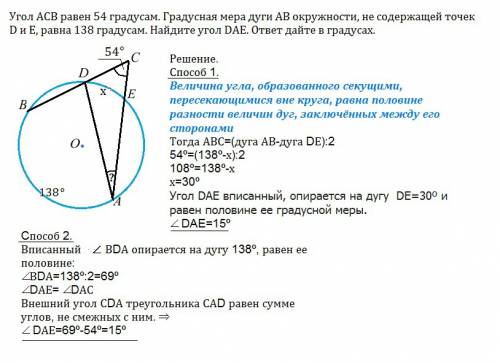
Угол ACB равен 54 градусам. Градусная мера дуги АВ окружности, не содержащей точек D и Е, равна 138 градусам. Найдите угол DAE. ответ дайте в градусах.
----------
Скорее всего, эта задача дается с готовым рисунком.
Угол АСВ образован секущими ВС и АС. пересекающим окружность с центром О в точках D и E
Решение.
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Тогда АВС=(дуга АВ-дуга DЕ):2
54º=(138º-х):2
108º=138º-х
х=30º
Угол DAE вписанный, опирается на дугу DЕ=30º и равен половине ее градусной меры.
∠ DAE=15º
Cпособ 2.
Вписанный угол ВDА опирается на дугу 138º, равен ее половине:
∠ВDА=138º:2=69º
∠DАЕ= ∠DАС
Внешний угол СDА треугольника САD равен сумме углов, не смежных с ним. ⇒
∠ DАЕ=69º-54º=15º
запишем уравнение прямой в виде y=k1*x+b
3y=-2x-4
y=(-2/3)x-4/3
а) запишем уравнение прямой параллельной данной
условием параллельности является k1=k2
y=(-2/3)x+b
подставляем точку М
1=(-2/3)*2+b b=1+4/3=2 1/3
y=(-2/3)x+ 2 1/3
б) условие перпендикулярности k1*k2=-1
k2=-1/(-2/3)=3/2
y=3/2x+b b=1-(3/2)*2=1-3=-2
y=3/2x-2
Подробнее - на -