Пошаговое объяснение:
Выясним, при каких значениях переменной функция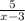 
не определена.
R ( x ) =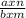 
, где n - степень числителя, а m - степень знаменателя.
Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
Если n = m , то горизонтальной асимптотой является прямая y = a b .
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m .
n = 0
m = 1
n < m , ось X, y = 0 , является горизонтальной асимптотой. y = 0
Вертикальные асимптоты: x = 3
Горизонтальные асимптоты: y = 0
Нет наклонных асимптот.
Существующие в современном обществе регуляторы подразделяются на две большие группы: социальные и технические. В юридической литературе также выделяются стихийные регуляторы.