Чему может быть равна площадь прямоугольника, если его периметр равен периметру квадрата со стороной 8 см?

👇

Увидеть ответ

Ответ:

aruka00000

15.02.2023

4x=2(x+y)

x=8

32=16+2y

y=8

S=x*y

S=8*8=64

4,5(22 оценок)

Ответ:

KristiDever

15.02.2023

Квадрат имеет самую большую площадь при заданном периметре.

1) Периметр квадрата по формуле:

P =4*a = 4*8 = 32 см - периметр

2) Периметр прямоугольника по формуле:

Р = 2*(a + b) = 32 см - по условию задачи.

a + b = 32 : 2 = 16 см - сумма длин двух сторон.

3) Площадь прямоугольника по формуле: S = a*b

Варианты: b = 16 - a - ширина

1) 1*15 = 15 см² и 2) 2*14 =28 см² и 3) 3*13 = 39 см² и 4) 4*12 = 48 см²

У квадрата площадь - 8*8 = 64 - самая большая.

4,6(99 оценок)

Открыть все ответы

Ответ:

LOLLLAada

15.02.2023

1. 1/2 или 4/8
2. Знаменатель дроби показывает на сколько равных долей делят, а числитель – сколько таких долей взято.
3. 1 г = 0,001кг
4. 1. чем больше знаменатель, тем меньше число
2. чем больше числитель, тем больше число
6. правильная дробь - это числитель меньше знаменателя 4/5, неправильная - это числитель больше знаменателя 6/3
7. Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители и оставить тот же знаменатель. Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби и оставить тот же знаменатель.
9. числитель делишь на знаменатель, целая часть-это целое число,
остаток от деления это числитель, а знаменатель тот же, -это называется выделить целую часть
10. 1+2/3
11. она будет неправильной
12. надо их перевести в неправильные дроби далее пункт 7
15. числитель*числитель/знаменатель*знаменатель
числитель*знаменатель/знаменатель*числитель
16. сначала пункт 12, а потом15
18. b/a
19. 0,23 0,67
21. Чтобы сравнить две десятичные дроби, нужно вначале сравнить их целые части. Та десятичная дробь больше (меньше), у которой целая часть больше (меньше).
23. Чтобы округлить десятичную дробь до определенного разряда целой или дробной части, все меньшие разряды заменяются нулями или отбрасываются, а предшествующий отбрасываемой при округлении цифре разряд не изменяет своей величины, если за ним идут цифры 0, 1, 2, 3, 4, и увеличивается на 1 (единицу), если идут цифры 5, 6, 7, 8, 9.
Извините, что некоторых номеров нет, но что не помню, того не помню.

4,8(62 оценок)

Ответ:

Ksushlalka

15.02.2023

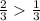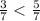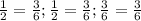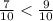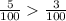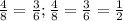
3. а) $\frac{2}{3}\frac{1}{3}$ б) $\frac{3}{7}$ в) $\frac{1}{2}=\frac{3}{6}; \frac{1}{2}=\frac{3}{6}; \frac{3}{6}=\frac{3}{6}$ г) $\frac{7}{10}$ д) $\frac{5}{100}\frac{3}{100}$ е) $\frac{4}{8}=\frac{3}{6}; \frac{4}{8}=\frac{3}{6}=\frac{1}{2}$