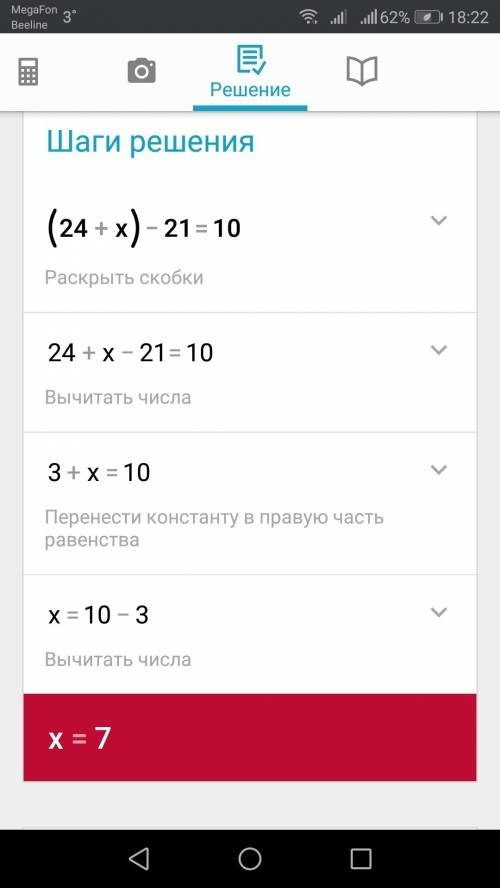
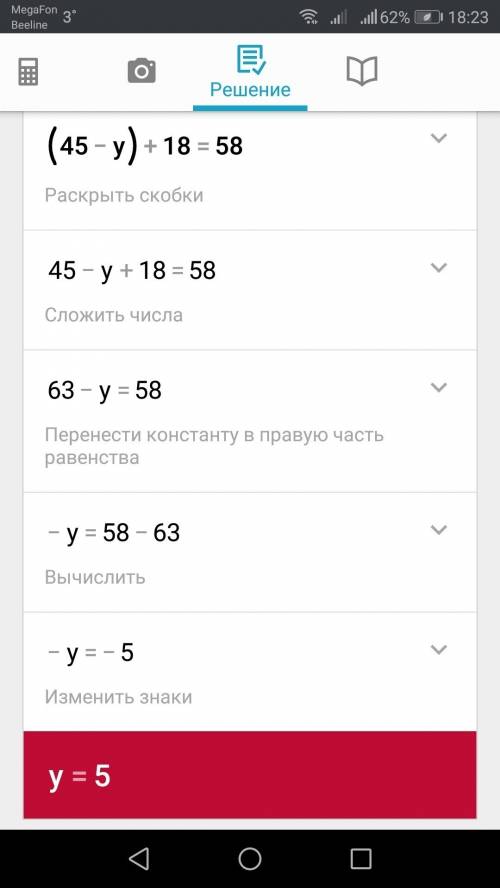
1)(24х+х)-21=10 2)(45-у)+18=58
24х+х-21=10 45-у+18=58
25х=10+21 у=58-18-45 -
25х=31 у= -5 -
х=31:25
х=1,24
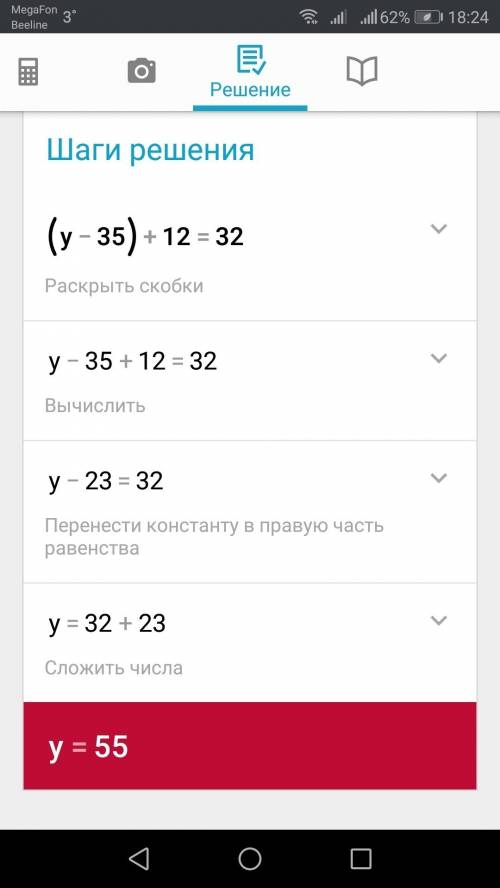
3)(у-35)+12=32
у-35+12=32
у=32-12+35
у=55
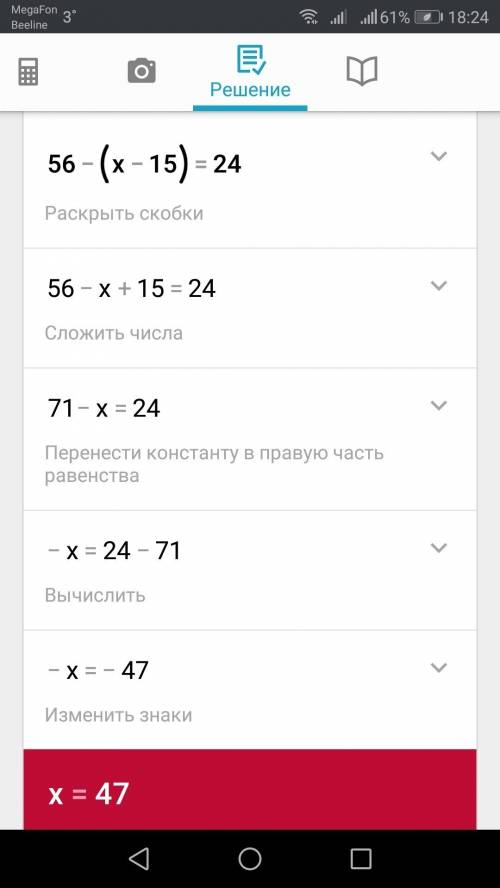
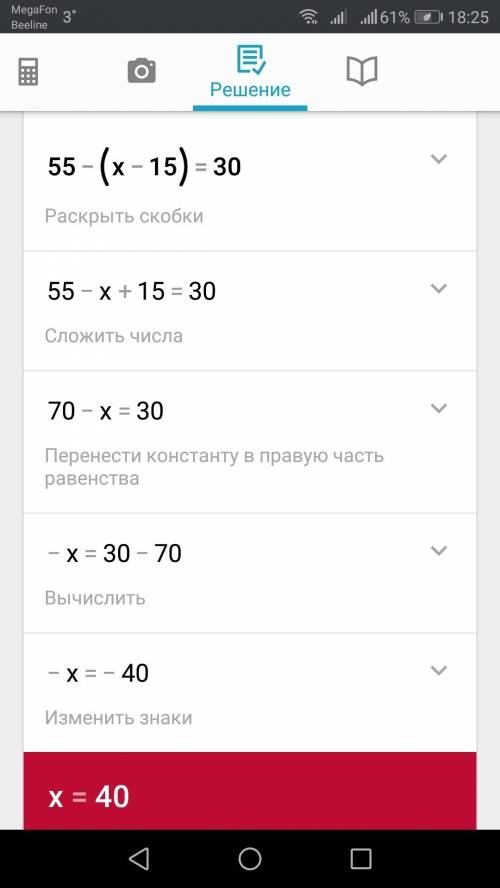
4)56-(х-15)=24
56-х+15=24
х=24-56-15
х=-47
5)24,55-(х-15)=30
24,55-х+15=30
-х=30-24,55-15
-х=-9,55
Пло́щадь — в узком смысле, площадь фигуры — численная характеристика, вводимая для определённого класса плоских геометрических фигур (исторически, для многоугольников, затем понятие было расширено на квадрируемыеПерейти к разделу «#Квадрируемые фигуры» фигуры) и обладающая свойствами площадиПерейти к разделу «#Свойства»[1]. Интуитивно, из этих свойств следует, что бо́льшая площадь фигуры соответствует её «большему размеру» (например, вырезанным из бумаги квадратом большей площади можно полностью закрыть меньший квадрат), a оценить площадь фигуры можно с наложения на её рисунок сетки из линий, образующих одинаковые квадратики (единицы площади) и подсчитав число квадратиков и их долей, попавших внутрь фигуры (на рисунке справа). В широком смысле понятие площади обобщается на k-мерные поверхности в n-мерном пространстве (евклидовом или римановом), в частности, на двумерную поверхность в трёхмерном пространствеПерейти к разделу «#Площадь поверхности».
Пошаговое объяснение: