Знак неравенства меньше нуля, значит, нужно, чтоб квадратичная функция была расположена ниже оси абсцисс. Для этого требуется установить направление ветвь параболы. Очевидно, же что, когда ветви параболы направлены вниз и D<0(дискриминант меньше нуля), неравенство выполняется для всех действительных значения х.
Получаем решение системы неравенств . То есть, при a ∈ (-∞;-6) неравенство (a+4)x²-2ax+2a-6<0 верно при всех действительных значения х. Наибольшее целое значение параметра а: а = -7.
а) пройдут январь, февраль, март, апрель - наступит 1 мая б) пройдут янв., февр., март, апрель, май и 10 дней июня - наступит 11 июня в) пройдут январь (31 дн.), февраль (28 дн.) и 28 дней марта - наступит 29 марта г) январь (31 дн.), февраль (28 дн.), март (31 дн.), апрель (30), май (31), июнь (30), июль (31) и 13 дней августа - наступит 14 августа д) пройдут 11 месяцев (31 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 31 + 3) и 24 дня ноября - наступит 25 ноября
Високосный год (на 1 день больше в феврале) :
а) 1 мая (количество дней не поменялось, т.к. считаем в месяцах) б) 11 июня (тоже считаем в месяцах) в) 30 марта (на 1 день больше, чем в простом году, т.к. в феврале + 1 день) г) 15 августа (на 1 день больше, чем в простом году) д) 26 ноября (на 1 день больше)
а) пройдут январь, февраль, март, апрель - наступит 1 мая б) пройдут янв., февр., март, апрель, май и 10 дней июня - наступит 11 июня в) пройдут январь (31 дн.), февраль (28 дн.) и 28 дней марта - наступит 29 марта г) январь (31 дн.), февраль (28 дн.), март (31 дн.), апрель (30), май (31), июнь (30), июль (31) и 13 дней августа - наступит 14 августа д) пройдут 11 месяцев (31 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 31 + 3) и 24 дня ноября - наступит 25 ноября
Високосный год (на 1 день больше в феврале) :
а) 1 мая (количество дней не поменялось, т.к. считаем в месяцах) б) 11 июня (тоже считаем в месяцах) в) 30 марта (на 1 день больше, чем в простом году, т.к. в феврале + 1 день) г) 15 августа (на 1 день больше, чем в простом году) д) 26 ноября (на 1 день больше)
Знак неравенства меньше нуля, значит, нужно, чтоб квадратичная функция была расположена ниже оси абсцисс. Для этого требуется установить направление ветвь параболы. Очевидно, же что, когда ветви параболы направлены вниз и D<0(дискриминант меньше нуля), неравенство выполняется для всех действительных значения х.
Получаем решение системы неравенств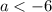 . То есть, при a ∈ (-∞;-6) неравенство (a+4)x²-2ax+2a-6<0 верно при всех действительных значения х. Наибольшее целое значение параметра а: а = -7.
. То есть, при a ∈ (-∞;-6) неравенство (a+4)x²-2ax+2a-6<0 верно при всех действительных значения х. Наибольшее целое значение параметра а: а = -7.