Question

Дан угол ϕ между диагоналями развёртки боковой поверхности цилиндра, и дана длина диагонали развёртки боковой поверхности b. определи площадь полной поверхности цилиндра.

Answer 1

Из прямоугольника, в котором задана длина диагонали b и угол Ф между диагоналями определим его стороны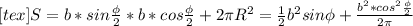 $<img src=$" alt="S = b*sin\frac{\phi }{2}*b*cos\frac{\phi }{2}+2\pi R^{2} =\frac{1}{2} b^{2} sin\phi +\frac{b^{2}*cos^{2}\frac{\phi}{2} }{2\pi}" />" /> (это высота цилиндра) и 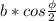$b*cos\frac{\phi }{2}$ (это длина окружности основания цилиндра).

Обозначим радиус окружности основания цилиндра через R, тогда можем записать:

$2\pi R=b*cos\frac{\phi}{2} \\R=\frac{b*cos\frac{\phi}{2}}{2\pi}$

Площадь полной поверхности цилиндра найдем как сумму боковой поверхности и двух оснований: