Пусть х тг. было у Алии, у тг. было у Дарии. Составим систему уравнений по условию задачи:
0,4х + 0,45у = 2150
0,45х + 0,4у = 2100
- - - - - - -
Сложим оба уравнения:
0,85х + 0,85у = 4250
- - - - - - -
Разделим обе части уравнения на 0,85:
х + у = 5000
х = 5000 - у
- - - - - - -
Подставим значение х в первое уравнение системы:
0,4 · (5000 - у) + 0,45у = 2150
2000 - 0,4у + 0,45у = 2150
0,45у - 0,4у = 2150 - 2000
0,05у = 150
у = 150 : 0,05
у = 3000 (тг.) - было у Дарии
- - - - - - -
х = 5000 - 3000
х = 2000 (тг.) - было у Алии
ответ: 2000 тг. и 3000 тг.
ДАНО
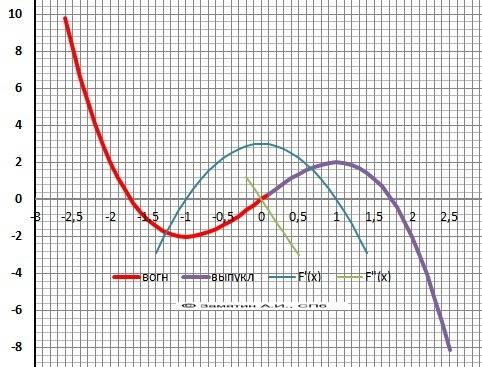
Y(x) = - x³ + 3x
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
2. Пересечение с осью Х. Y=0 при х = -√3, 0, √3.
Положительна - X∈(-∞;-√3)∪(0;√3), отрицательна - X∈(-√3;0)∪(√3;+∞).
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = -∞
5. Исследование на чётность.Y(-x) = x³-3*x = - Y(x).
Функция нечётная.
6. Производная функции.Y'(x)= -3*x² +3 = -3*(x²-1) = -3*(x-1)(x+1).
Корни при Х= +/- 1. Схема знаков производной.
(-∞)__(<0)__(-1)___(>0)___(1)__(<0)_____(+∞)
7. Локальные экстремумы.
Максимум Ymax(1)= 2, минимум – Ymin(-1)=2.
8. Интервалы возрастания и убывания.
Возрастает - Х∈[-1;1], убывает = Х∈(-∞;-1]∪ (1;+∞).
8. Вторая производная - Y"(x) = -6*x=0.
Корень производной - точка перегиба Y"(x)= 0.
9. Выпуклая “горка» Х∈(0;+∞), Вогнутая – «ложка» Х∈(-∞;0).
10. График в приложении.
1) 8+(76-50)=8+26=34
2) (15-7)+29=8+29=37