Поскольку корзины были одинаковые, а со второго участка собрали больше корзин, чем с первого (60 ˃ 51), значит, разница в массе винограда приходится на разницу в количестве корзин, собранных с первого и второго участков.
1) Найдем, на сколько корзин больше собрали со второго участка, чем с первого: 60 – 51 = 9 (к.);
2) Вычислим, сколько кг винограда было в одной корзине: 216 : 9 = 24 (кг);
3) Узнаем, сколько кг винограда собрали с первого участка: 24 · 51 = 1224 (кг);
4) Определим, сколько кг винограда собрали со второго участка: 24 · 60 = 1440 или 1224 + 216 = 1440 (кг).
ответ: с первого участка собрали 1224 кг винограда, а со второго – 1440 кг.
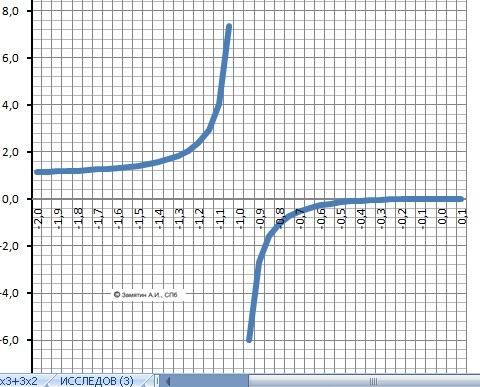
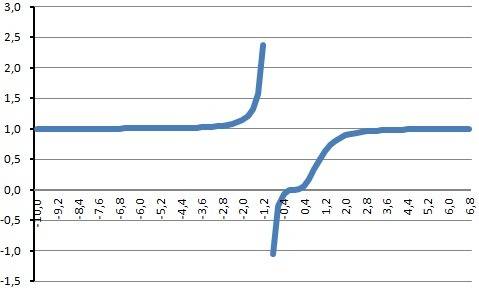
1.Область определения - Х∈(-∞;-1)∪(-1;+∞). Разрыв при Х=-1
2. Пересечение с осью Х. Y=0 при х =1.
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞
5. Исследование на чётность.Y(-x) ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.
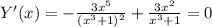
7. Корень при Х1=0.
Максимумов - нет, минимумов - нет .Возрастает - Х∈(-∞;+∞)
8. Точка перегиба Y"(x)=0 при X=-1
9. График в приложении. На втором - участок около х = -1.
ДАНО
Y = lnX/X
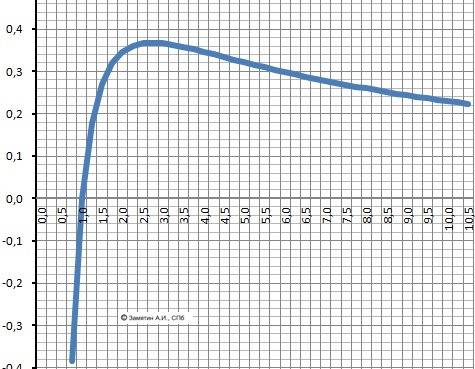
Область определения - Х∈(0;+∞)
2. Пересечение с осью Х. Y=0 при х = 1.
3. Пересечение с осью У - нет 9.
4. Поведение на бесконечности.limY(0+) = - ∞ limY(+∞) = е
5. Исследование на чётность. Y(x) ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.
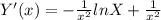
7. Корни при Х1=e. Максимум Ymax= 1/e.
Возрастает - Х∈(0;e), убывает = Х∈(e;+∞).
8. Вторая производная.
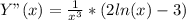
9. Точка перегибаY"(x)=0 при z=∛e².
Выпуклая “горка» Х∈(0;z),Вогнутая – «ложка» Х∈(z;+∞).
10. График в приложении
ответ: увеличится
Пошаговое объяснение:
При делении 1 на 14 получается периодическая дробь 0,0(714285)
При повторении периода 333 раза мы дойдём до 1999 знака (до 5) а 2003 знаком будет 2. Если 2 удалить, то на её место встанет 8, т. е. дробь увеличится.