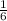, 
нам "говорит" о том, что это следующий подъезд, 4 подъезда по 12 квартир получается 48, а т.к. Глеб живет в 50 квартире, то это уже сдедующий подъезд, т.е. 5. А т.к. квартир на каждом этаже по 3, то следовательно получаем те 2 квартиры, которые остались находятся на 1 этаже. ответ: Глеб живет в 5 подъезде на 1 этаже
ответ: 30% и 60%.
Пошаговое объяснение:
Пусть M1 кг и M2 кг - массы первого и второго сплавов, а x% и y% - процентное содержание меди в них. Тогда масса меди в первом сплаве m1=M1*x/100 кг, а во втором сплаве - m2=M2*y/100 кг. Если сплавить 1 кг первого сплава с 2 кг второго сплава, то получится сплав массой M3=1+2 =3 кг, а так как по условию меди в нём - 50%, то её масса в этом сплаве m3=M3*50/100=1,5 кг. Если же сплавить 4 кг первого сплава с 1 кг второго сплава, то получится сплав массой M4=4+1=5 кг, а так как по условию меди в нём - 36%, то её масса в этом сплаве m4=M4*36/100=1,8 кг. Но в одном килограмме первого сплава находится x/100 кг меди, в 4-х кг - 4*x/100 кг меди, в 1 кг второго сплава - y/100 кг меди и в 2 кг этого сплава- 2*y кг меди. Отсюда следует система уравнений:
x/100+2*y/100=1,5
4*x/100+y/100=1,8
или
x+2*y=150
4*x+y=180
Решая её, находим x=30% и y=60%.
Посчитаем количество квадратов по горизонтальной стороне стороне
an = 120/120 = 1 - последний (n-й) член ариф. прогрессии
a₁= 4/120 -первый член ариф. прогрессии (для горизонтальной стороны)
d = 4/120 - разность ариф. прогрессии (для горизонтальной стороны)
n - количество членов ариф. прогрессии (количество квадратов)
an = a₁ + (n-1)*d
1 = 4/120 + (n-1)*4/120
1= 4/120 + (4/120)*n - 4/120
1 = (4/120)*n
n = 1 : (4/120) = 1*120/4 = 30 - количество членов ариф. прогрессии (количество квадратов) - ВЕРНО
ответ: 30 квадратов