ответ: 58 ед.² - наибольшая площадь поверхности.
Решаем силой Разума - сначала думаем.
Мысль 1. Если у фигуры - шар и куб имеют самую малую площадь поверхности, то противоположная фигуру -будет иметь самую большую площадь поверхности.
Мысль 2. Для фигуры из кубиков это будет параллелепипед из кубиков выстроенных в один ряд.
Расчет: фигура - параллелепипед со сторонами:
a = 14 - длина - больше чёрных кубиков нет.
b = c = 1 - ширина и высота - кубиков.
Площадь поверхности параллелепипеда по формуле:
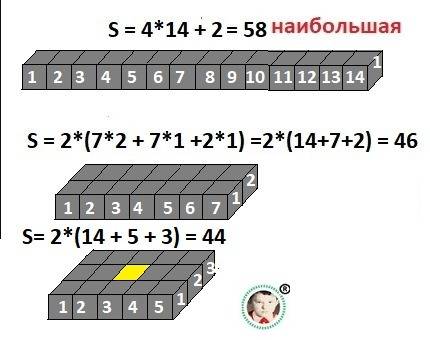
S = 2*(a*b + a*c + b*c) = 4*14 + 2*1 = 56 + 2 = 58 (ед.²) - площадь - ответ.
Рисунок к задаче - в приложении.
Дополнительно и без большого труда вычислим площадь других подобных фигур. Два варианта на рисунке.
Вывод: наша мысль 2 - правильная. Чем больше фигура стремится к кубу, тем меньше у неё площадь поверхности.
Пусть x - количество однорублёвых монет, y - двухрублёвых, а z - пятирублёвых. Тогда получается такая система уравнений:
1x + 2y + 5z = 34
x + y + z = 15
x = y + z + 1
Подставим x во второе уравнение, например:
y + z + 1 + y + z = 15
2y + 2z = 15 - 1
2y + 2z = 14
y + z = 7
Теперь выразим напр. у:
y = 7 - z
И подставим х и у в первое уравнение:
y + z + 1 + 2(7 - z) + 5z = 34
7 - z + z + 1 + 14 - 2z + 5z = 34
3z = 34 - 7 - 1 - 14
3z = 12
z = 4
Подставим в уравнение с выраженным y:
y = 7 - 4
y = 3
ответ: У Лизы 3 двухрублёвые монеты
48 чисел
Пошаговое объяснение:
Даны цифры 1, 2, 3, 4, и 5
Составляем из этих цифр числа кратные числу 6, т.е. числа, которые делятся на 6 без остатка.
Признак делимости на 6: чтобы число делилось на 6, надо, чтобы оно делилось на 2 и на 3 одновременно, т.е. число должно быть чётное и сумма его цифр должна делиться на 3.
Двузначные числа: 12, 42, 42, 54 - всего 4 числа
Составляем трёхзначные числа. Берём тройки цифр, в сумме дающие число 6: {1,2,3}, {2,3,4}, {3,4,5}, учитывая, что на месте единиц должна быть чётная цифра. Получаем 8 таких чисел: 132, 234, 324, 342, 432, 354, 534.
Составляем четырёхзначные числа из цифр {1,2,4,5}. В призовём комбинаторику. Имеем два чётных числа. Их "закрепляем" на месте единиц, на место десятков ставим любое из оставшихся трёх чисел (4-1=3), на место сотен - любое из оставшихся двух (3-1=2), на место тысяч - одно число. Полученные варианты перемножаем, получаем количество таких чисел 1*2*3*2=12
Составляем пятизначные числа, используя все цифры {1,2,3,4,5}. 1+2+3+4+5=15 делится на 3. Среди чисел имеем два чётных - это 2 и 4. В опять призываем комбинаторику:
1*2*3*4*2 = 24 числа
Шестизначные и далее составить не можем, т.к. цифры в числе не должны повторяться.
Получаем всего 4+8+12+24 = 48 чисел кратных 6
Пошаговое объяснение:
Черный единичный кубик мистера Фокса имеет 6 черных граней единичной площади.
Если Мистер Фокс строит параллелепипед, стараясь, чтобы он был красивым при наибольшей площади черной области, то он должен:
1. разместить черные кубики в вершинах параллелепипеда. Там их черные грани будут располагаться в трех гранях построенного параллелепипеда, т.е. видны будут три грани из шести . Т.е. в каждой вершине параллелепипеда, а их 8, будет черный кубик, с видимой площадью черной области 3 ед. пл. Это кубики а на рис. 1.
3*8 = 24 ед.пл. ---- площадь черной области в вершинах параллелепипеда.
2. 14 - 8 = 6 кубиков, которым не хватило места в вершинах. Их мистер Фокс должен располагать на ребрах, так, чтобы две единичные черные грани располагались на двух соседних гранях параллелепипеда. Всего ребер в параллелепипеде 12, надо только, чтобы их длина была больше двух единичных отрезков, чтобы можно было разместить кубики между вершинами. Это кубики б, показывающие черные участки 2 ед. пл
2 * 6 = 12 ед.пл. ---- площадь черных областей на ребрах кубиков б
24 + 12 = 36 ед. пл ---- максимально возможная площадь черной области при таком построении
Но, если мистер Фокс задался целью построить параллелепипед с максимально возможной общей площадью, он, желая, чтобы черный кубик показывал максимальное число черных граней, составит их в один ряд, (рис. 2) Два крайних 1-ый и 14-ый (тип M) покажут 5 граней из 6, т.е.
5 * 2 = 10 ед.пл. ----- их общая площадь
14 - 2 = 12 --- число кубиков в середине (тип N)
Кубики в середине, с 2-го по 13-ый, покажут только 4 грани.
4 * 12 = 48 ед.пл. ------ суммарная площадь видимой поверхности черных кубиков в середине.
10 + 48 = 58 ед. пл. ---- суммарная возможная площадь.
Мистер Фокс может располагать в ряду между черными кубиками любое число белых, но на суммарную площадь черной области это влиять не будет.