Привет это Настя с тобой в одном классе учусь. 100 минут
Пошаговое объяснение:
Решим задачу. Два заводских автобуса, двигаясь по разным маршрутам, проезжают одну и ту же остановку. Первый – через 20 минут, второй – через 50 минут. Через какое наименьшее время они встретятся на этой остановке, выезжая с неё одновременно?
Решение: чтобы решить эту задачу, нужно расписать время проезда первого и второго автобуса и найти минимальный одинаковый промежуток времени.
Время, которое нужно для проезда до нужной остановки первым автобусом: 20 мин.; 40 мин.; 60 мин.; 80 мин.; 100 мин. и т. д.
Время, которое нужно для проезда до нужной остановки вторым автобусом: 50 мин.; 100 мин.; 150 мин. и т. д.
Как видно из рассуждений, время совпадёт первый раз в 100 мин. Это и есть решение задачи.
ответ: 100 мин.
3 часа 20 минут плыла лодка по течению
93 целые 1/3 км все расстояние
Пошаговое объяснение:
Пусть х км расстояние в одном направлении. Тогда скорость лодки по течению равно 12+2=14 км/ч, а против течения 12-2=10 км/ч. Время которое лодка потратила по направлению течения равно х/14ч, а против течения х/10 ч. Всего на весь пусть затратила 8 часов. Составим уравнение:
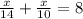
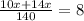
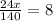
24x=140*8
24x=1120
x=1120/24=46 2/3 км в одном направлении
1) 140/3:14=10/3= 3 целые 1/3= 3 часа 20 минут плыла лодка по течению
2) 140/3*2=93 целые 1/3 км все расстояние
Пусть 3^x=t,3
x
=t, t > 0,t>0, \sqrt{t^2-5a}=t-a.√
t
2
−5a
=t−a.
При t-a < 0t−a<0 правая часть уравнения отрицательная, а левая — неотрицательная, поэтому уравнение при t < at<a решений не имеет.
При t-a \geq 0t−a≥0 получаем t^2-5a=t^2-2at+a^2t
2
−5a=t
2
−2at+a
2
, 2at=a^2+5a2at=a
2
+5a.
При a=0\;a=0 2 \cdot 0 \cdot t =02⋅0⋅t=0 — любое положительное значение t является корнем уравнения, что противоречит условию единственности корня.
При a \neq 0\;a≠0 \displaystyle t=\frac{a+5}{2}t=
2
a+5
. Для этого корня должны выполняться условия t \geq at≥a и t > 0t>0.
Условие \displaystyle \frac{a+5}{2} \geq a
2
a+5
≥a выполняется при a \leq 5a≤5.
Условие \displaystyle \frac{a+5}{2} > 0
2
a+5
>0 выполняется при a > -5a>−5.
Исходное уравнение имеет единственный корень при -5 < a < 0−5<a<0 и 0 < a \leq50<a≤5.
ответ
(-5;0)\cup (0;5](−5;0)∪(0;5]