Сравним значения выражения сначала и после приведённых в условии действий. 
и 
- начальные значения,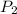 
и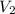 
- конечные. Так как по условию 
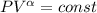, то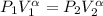 
. По условию объём газа уменьшили в 64 раза, то есть, 
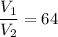, из-за этого давление газа
увеличилось не менее, чем в 8 раз, то есть,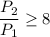 
. Из уравнения
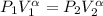составляем пропорцию: 
. По свойству степени, 
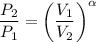. Так как 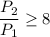, то:
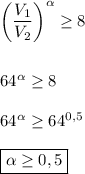
Таким образом, наименьшее значение константы 
, при котором уменьшение объёма газа в 64 раза приводит к увеличению давления не менее, чем в 8 раз: 0,5.
ответ: 0,5.
Пошаговое объяснение:
Проверить сходимость ряда можно несколькими Во-первых можно просто найти сумму ряда. Если в результате мы получим конечное число, то такой ряд сходится. Например, поскольку
то данный ряд сходится. Если нам не удалось найти сумму ряда, то следует использовать другие методы для проверки сходимости ряда.
Одним из таких методов является признак Даламбера, который записывается следующим образом:
здесь и соответственно и члены ряда, а сходимость определяется значением . Если - ряд сходится, если - расходится. При - данный признак не даёт ответа и нужно проводить дополнительные исследования.
В качестве примера, исследуем сходимость ряда ∞n0n4n с признака Даламбера. Сначала запишем выражения для ann4n и an1n14n1 . Теперь найдем соответствующий предел:
limn∞an1anlimn∞n14n4n1nlimn∞n14n14limn∞11n14
Поскольку 14<1 , в соответствии с признаком Даламбера, ряд сходится.
Еще одним методом, позволяющим проверить сходимость ряда является радикальный признак Коши, который записывается следующим образом:
limn∞nanD
здесь an n-ый член ряда, а сходимость, как и в случае признака Даламбера, определяется значением D: Если D < 1 - ряд сходится, если D > 1 - расходится. При D = 1 - данный признак не даёт ответа и нужно проводить дополнительные исследования.
В качестве примера, исследуем сходимость ряда ∞n05n12n56n2 с радикального признака Коши. Сначала запишем выражение для an5n12n56n2 . Теперь найдем соответствующий предел:
limn∞nanlimn∞n5n12n56n2limn∞5n12n56n2nlimn∞5n12n562nlimn∞5n1n2n5n62nlimn∞51n25n62nlimn∞51n25n6limn∞51n25n2n5261562564
Поскольку 1562564>1 , в соответствии с радикальным признаком Коши, ряд расходится.
Стоит отметить, что наряду с перечисленными, существуют и другие признаки сходимости рядов,
y=9,8
Пошаговое объяснение:
y–4/7y=4,2
7/7y-4/7y=4,2
3/7y=4,2
y=4,2:3/7
y=21/5*7/3=49/5=9,8