Дано:
- точки, принадлежащие плоскости П: О(0; 0; 0), М(0; 2; –2), N(2; 2; 2),
- плоскость yOz.
Находим векторы:
ОМ = (0; 2; –2), ОN (2; 2; 2).
Нормальный вектор n плоскости П равен векторному произведение векторов ОМ и ОN.
i j k| i j
0 2 -2| 0| 2
2 2 2| 2 2 = 4i - 4j + 0k - 0j + 4i - 4k = 8i - 4j - 4k.
n = (8; -4; -4).
У координатной плоскости yOz нормальным вектором является координатный вектор k=(1; 0; 0).
Находим косинус угла α между нормальными векторами плоскостей П и плоскостью yOz это и будет угол между заданными плоскостями.
Сначала надо определить модули векторов:
|n| = √(8² + (-4)² + (-4)²) = √(64 + 16 +16) = √96 = 4√6.
|k| = 1.
cos α = (8*1 + -4*0 + -4*0)/(4√6*1) = 8/4√6 = 2/√6 = √(2/3).
α = arc cos(√(2/3)) = 0,61548 радиан или 35,26439 градуса.
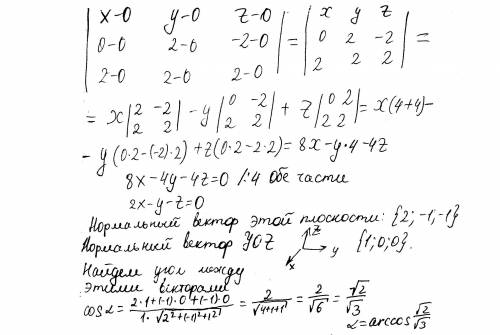
3 дня и 6 дней
Пошаговое объяснение:
Задание
Двое рабочих, работая вместе, закончили работу за 2 дня. За сколько дней выполнит эту работу каждый из них, работая отдельно, если известно, что если бы первый работал 2 дня, а второй работал 1 день, то вместе они бы выполнили 5/6 всей работы.
Решение
Пусть х - количество дней, в течение которых выполнит работу 1-й рабочий, а у - количество дней, в течение которых выполнит работу второй рабочий. Принимаем всю работу за 1. Тогда производительность труда первого рабочего составляет 1/х, а второго 1/у.
Работая вместе в течение 2-х дней, рабочие выполнили всю работу:
(1/х + 1/у) · 2 = 1 (уравнение 1)
Во втором случае:
(2/х + 1/у) = 5/6 (уравнение 2)
Умножим левую и правую части уравнения (2) на 6:
12/х +6/у = 5 (уравнение 3)
Умножим левую и правую части уравнения (1) на 6:
12/х +12/у = 6 (уравнение 4)
Из уравнения (4) вычтем уравнение (3)
(12/х - 12/х) + (12/у - 6/у) = (6-5),
6/у = 1,
у = 6.
Полученное значение у подставим в уравнение (2):
2/х + 1/6 = 5/6
2/х = 5/6 - 1/6
2/х = 4/6
х = 2 · 6 : 4 = 3
ответ: первый рабочий, если будет работать один, выполнит всю работу за 3 дня, а второй рабочий, если будет работать один, - выполнит ту же работу за 6 дней.
ответ:10
Пошаговое объяснение:
18:3=6 6 в 4 раза меньше 10
Товет 10