1)Воспользуемся формулой члена арифметической прогрессии, который стоит на n-м месте аn = a1 + (n - 1) * d.
В условии задачи сказано, что член данной последовательности под номером один равен -15, а разность данной арифметической прогрессии равна 3.
Подставляя эти значения, а также значение n = 23 в формулу члена арифметической прогрессии, который стоит на n-м месте, находим двадцать третий член данной арифметической прогрессии:
а23 = -15 + (23 - 1) * 3 = -15 + 22 * 3 = -15 + 66 = 51.
ответ: двадцать третий член данной арифметической прогрессии равен 51.
Пошаговое объяснение:
2)Первые 10 членов арифметической прогрессии:-4; -2; 0; 2; 4; 6; 8; 10; 12; 14Так как сумма первых пяти членов прогрессии равна нулю:-4 +(-2) + 0 + 2 + 4 = 0То сумма первых десяти членов будет равна сумме последующих пяти членов прогрессии:6 + 8 + 10 + 12 + 14 = 50
Единичный отрезок разбит на 3 части, значит в одном маленьком делении содержится 1/3 единицы измерения (цена деления = 1/3 ) .
Точка Е находится на расстоянии 1/3 от 0 вправо ( в положительном направлении) . Значит координата точки Е - это 1/3 , обозначаем так Е(1/3) .
Точка A находится на расстоянии 1/3 от 0 влево ( в отрицательном направлении) . Значит координата точки А - это -1/3 , обозначаем так А(-1/3) .
Точка F находится на расстоянии 2/3 от 1 вправо ( в положительном направлении) . Значит координата точки F - это 1 +2/3=1 целая и 2/3 , обозначаем так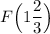 .
.
Аналогично, определяем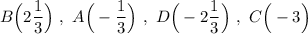 .
.