Лемма: рассмотрим числа, в записи которых отсутствует 0. Тогда при умножении этого числа на 8 сумма его цифр увеличится не более чем в 8 раз.
Доказательство: предположим противное. Пусть - сумма цифр числа n, а - количество цифр числа n. Тогда , где , с другой стороны , значит, , что неверно для . Если , то число n состоит только из единиц, а число 8n - из девяток, что, очевидно, неверно. Лемма доказана.
Рассмотрим теперь произвольное число x, где есть нули. Выберем такое число y, что во всех отличных от нуля цифрах числа x оно с ним совпадает, а в нулевых цифрах у него единицы (например, для числа x=8048903 число y было бы 8148913). Тогда - есть число, состоящее из 1 и 0. В свою очередь состоит из 8 и 0.
Если , то применяя лемму, получим , с другой стороны , что видно из механизма умножения в столбик таких чисел. Противоречие.
Решение: Обозначим скорость вытекания второй трубы за (х)л/мин, тогда скорость вытекания первой трубы, согласно условия задачи, равна: (х-1)л/мин Первая труба наполняет бассейн за время: 110/(х-1) мин Вторая труба наполняет бассейн за время: 99/х мин А так как первая труба заполняет бассейн на 2 мин дольше чем вторая составим уравнение: 110/(х-1)-99/х=2 х*110-(х-1)*99=(х)*(х-1)*2 110х-99х+99=2x^2-2x 2x^2-2x-110x+99x-99=0 2x^2-13x-99=0 x1,2=(13+-D)/2*2 D=√(169-4*2*-99)=√(169+792)=√961=31 x1,2=(13+-31)/4 x1=(13+31)/4 x1=44/4 x1=11 (л/мин) - скорость вытекания трубы второй трубы x2=(13-31)/4 x2=-18/4 x2=-4,5 не соответствует условию задачи Отсюда: скорость вытекания первой трубы: (х-1) или: 11-1=10 л/мин
Лемма: рассмотрим числа, в записи которых отсутствует 0. Тогда при умножении этого числа на 8 сумма его цифр увеличится не более чем в 8 раз.
Доказательство: предположим противное. Пусть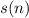
- сумма цифр числа n, а 
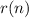- количество цифр числа n. Тогда ![r(8n)\geq [\frac{\alpha s(n)}{9}]](/tpl/images/0643/9493/ec9f5.png)
, где 
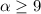, с другой стороны 
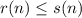, значит, ![s(n)\geq[\frac{\alpha s(n)}{9}]](/tpl/images/0643/9493/9e110.png)
, что неверно для 
. Если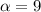 
, то число n состоит только из единиц, а число 8n - из девяток, что, очевидно, неверно. Лемма доказана.
Рассмотрим теперь произвольное число x, где есть нули. Выберем такое число y, что во всех отличных от нуля цифрах числа x оно с ним совпадает, а в нулевых цифрах у него единицы (например, для числа x=8048903 число y было бы 8148913). Тогда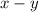
- есть число, состоящее из 1 и 0. В свою очередь 
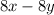состоит из 8 и 0.
Если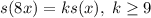
, то применяя лемму, получим 
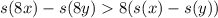, с другой стороны 
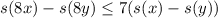, что видно из механизма умножения в столбик таких чисел. Противоречие.
Пример: 1*8=8
Задача про минимум решается аналогично