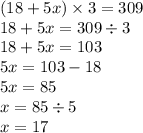
ответ:
пошаговое объяснение:
а)(9 1/4-8 2/3)×1 5/7+(4 2/9-2 5/6): 1 1/9
выполняем по правилам - сначала в скобках, потом умножение, деление за скобками, и затем складываем результаты:
9 1/4-8 2/3 = 37/4-26/3 = (111-104)/12 = 7/12 4 2/9-2 5/6 = 38/9-17/6 = (228-153)/54 = 75/54 7/12 × 1 5/7 = 7/12×12/7 = 1 75/54: 1 1/9=75/54: 10/9=75/54×9/10 = (75×9)/54×10 = 25/12 = 2 1/12ответ: получается 2 1/12
б)2 3/11×7/9 + 6 8/11: 1 2/7 - 1 1/8
здесь тоже по правилам - умножение, деление, сложение и вычитание:
2 3/11×7/9 = 25/11×7/9 = 175/99 6 8/11: 1 2/7 = 74/11: 9/7 = 74/11×7/9 = 518/99 175/99+518/99 = 693/99 = 7 7-1 1/8 = 6 8/8-1 1/8 = 5 7/8Пошаговое объяснение:
Проведем из вершины В параллелограмма высоты ВК и ВН к сторонам АД и СД.
Так как у параллелограмма длины противоположных сторон равны, то АД = ВС = 18 см, СД = АВ = 12 см.
Применим формулу площади параллелограмма.
S = АД * ВК и S = СД * ВН.
S = 18 * ВК = 144.
ВК = 144 / 18 = 8 см.
Из прямоугольного треугольника МВК, по теореме Пифагора, определим длину гипотенузы МК.
МК2 = ВК2 + МВ2 = 82 + 122 = 64 + 144 = 208.
МК = 4 * √13 см.
S = СД * ВН.
S = 12 * ВН = 144.
ВК = 144 / 12 = 12 см.
Из прямоугольного треугольника МВН, по теореме Пифагора, определим длину гипотенузы МН.
МН2 = ВН2 + МВ2 = 122 + 122 = 144 + 144 = 228.
МН = 2 * √12 см.
ответ: Расстояния от точки M до прямой AД равно 4 * √13 см, до прямой CД равно 2 * √12 см.
ответ:x=17
Пошаговое объяснение: