![\int \frac{\sqrt{x}\, dx}{\sqrt{x}+1}=[\; t=\sqrt{x}\; ,\; x=t^2\; ,\; dx=2t\, dt\; ]=\int \frac{t\cdot 2t\, dt}{t+1}=2\int \frac{t^2\, dt}{t+1}=\\\\=2\int (t-1+\frac{1}{t+1})dt=2\cdot (\frac{t^2}{2}-t+ln|t+1|)+C=\\\\=x-2\sqrt{x}+2\, ln|\sqrt{x}+1|+C](/tpl/images/0977/4335/89021.png)
Пошаговое объяснение:
√x=t ; x=t² ; (x)'=(t²)' ; dx=2tdt
∫ (t2t/(t+1))dt=∫2(t²/(t+1))dt для упрощения дроби к числителю прибавим и отнимем t+1
2∫((t²+t-t-1+1)/(t+1))dt=2∫(t(t+1)-(t+1)+1)/(t+1))dt=2∫(t-1+(1/(t+1))dt=2∫tdt-2∫dt+2(1/(t+1))dt=2(t²/2)-2t-2∫(1/(t+1)d(t+1)=t²-2t+2LnIt+1I+c=x-2√x+2ln(√x+1)+c
60 машин было первоначально на первой стоянке
300 машин было первоначально на второй стоянке
Пошаговое объяснение:
Если на первой автостоянке было в 5 раз меньше машин, чем на второй, значит на второй было в 5 раз больше машин, чем на первой.
Пусть на первой стоянке было х машин, тогда на второй стоянке 5х машин (в 5 раз больше, чем на первой)
Когда со второй стоянки на первую перевели 120 автомобилей, машин на стоянках стало поровну.
Составим уравнение:
5х - 120 = х + 120
5х - х = 120 + 120
4х = 240
х = 240/4
х = 60 (машин) было на первой стоянке
60*5 = 300 (машин) было на второй стоянке
Проверим:
300 - 120 = 60 + 120
180 = 180
Представить число 7 в виде суммы трех натуральных слагаемых можно следующими с точностью до порядка слагаемых):
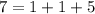

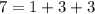

Представления первыми двумя не могут соответствовать сторонам треугольника, так как для них не выполняется неравенство треугольника. Заметим, что 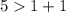 и
и 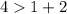 , хотя каждая сторона треугольника должна быть меньше суммы двух других сторон.
, хотя каждая сторона треугольника должна быть меньше суммы двух других сторон.
Значит, треугольник имеет стороны 1, 3, 3 или 2, 2, 3. Каких-либо других ограничений на сторону АВ нет, поэтому она может иметь длину 1, 2 или 3.
ответ: 1, 2 или 3