x dx 1 2x dx 1 d(7+x²) 1
∫ = ∫ = ∫ = ln(7+x²)+C
7+x² 2 7+x² 2 7+x² 2
[1/2 *ln(7+x²)+C ]¹= 1/2*[ 2x /(7+x²)+0]= x /(7+x²)
x+18 (x-2)+20 1 2(x-2) dx
2) ∫dx=∫ dx= ∫ dx+20 ∫ =
x²-4x-12 (x-2)²-16 2 (x-2)²-16 (x-2)²-16
1 1 | x-2-4 | 1 5 | x-6 |
= *ln|(x-2)²-16|+20 * *ln || +C= *ln |x²-4x-12|+*ln || +C
2 2*8 | x-2+4 | 2 4 | x+2 |
3) ∫(3-x) cosx dx=[ u=3-x , du=-dx , dv=cosx dx , v=sinx ] =(3-x)sinx+∫ sinx dx=
=(3-x)sinx-cosx+C
[(3-x)sinx-cosx]¹= -sinx+(3-x)cosx+sinx +0=(3-x)cosx
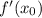
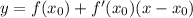

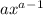 - где а- степень
- где а- степень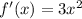 - вот такая вот производная
- вот такая вот производная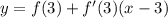
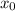 :
: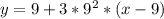
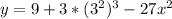
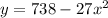
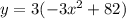 - это и есть касательная в ДАННОЙ точке.
- это и есть касательная в ДАННОЙ точке.
х+4х=32
5х=32/5
х=62
4х62=
Пошаговое объяснение:
х+2х=32
3х=32/3
х=102
2х102=