Дана функция f(x) = 8x^3+9x^2+3x+2.
Её производная равна y' = 24x^2 + 18x + 3 = 3(8x^2 + 6x + 1).
Приравняем её нулю (достаточно выражение в скобках):
8x^2 + 6x + 1 = 0, Д = 36 - 4*8*1 = 4,
х1 = (-6 - 2)/(2*8) = -1/2,
х2 = (-6 + 2)/(2*8) = -1/4.
Найдены 2 критические точки.
Определяем их свойства по знаку производной левее и правее этих точек.
x = -0,6 -0,5 -0,4 -0,25 -0,2
y' = 0,84 0 -0,36 0 0,36.
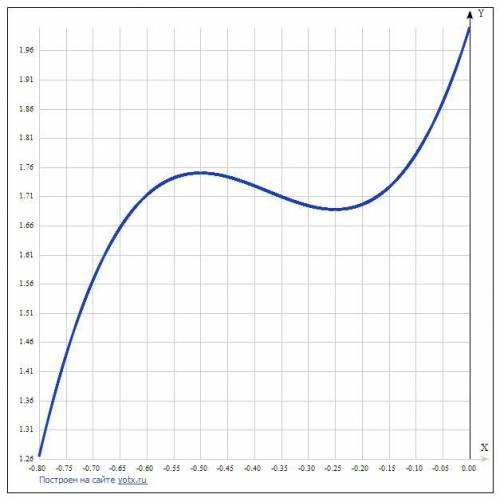
Как видим, максимум в точке х = -0,5, а минимум в точке х = -0,25.
Значения функции в критических точках:
y(min) = 27/16 при x = -1/4,
y(max) = 7/4 при x = -1/2.
Пошаговое объяснение:
1)
х(х+7)≥0
Найдем корни уравнения:
х(х+7)=0
х=0 ; х=-7
Метод интервалов.
[-7][0] (точки закрашены)
х∈(-∞;-7]∪[0 ;+∞)
2)
(х-1)(х+2)≤0
х=1 ; х=-2
Метод интервалов:
[-2][1] точки закрашены
х∈[-2;1]
3)
-х²+х+2<0
х²-х-2>0
х₁₂=(1±√(1+8))/2
х₁=2 ; х₂=-1.
(х-2)(х+1)>0
Метод интервалов:
(-1)(2) точки пустые
х∈(-∞;-1)∪(2;+∞).
4)
-х²-5х+6>0
х²+5х-6<0
х₁=1 ; х₂=-6
Равносильное неравенство:
(х-1)(х+6)<0
Метод интервалов:
(-6)(1) ( точки пустые)
х∈(-6 ; 1).
5) Перемножим:
х²+2х-15<0
х₁₂=-1±√16
х₁=-1+4=3.
х₂=-1-4=-5
(х-3)(х+5)<0
Метод интервалов:
(-5)(3) (точки пустые)
х∈(-5; 3).
S=2(2см*4см)+2(2см*14см)+2(4см*14см)
S=16кв.см+56кв.см+112кв.см
S=184кв.см-площадь поверхности