1. некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. сначала вычисляется длина исходной цепочки символов; если она чётна, то удаляется правый символ цепочки, а если нечётна, то в начало цепочки добавляется буква б. в полученной цепочке символов каждая буква
заменяется буквой, следующей за ней в алфавите (а — на б; б — на в и т.д., а я — на а).получившаяся таким образом цепочка является результатом работы описанного алгоритма.например, если исходной была цепочка авс, то результатом работы алгоритма будет цепочка вбгт, а если исходной была цепочка
крот, то результатом работы алгоритма будет цепочка лсп.дана цепочка символов стоп. какая цепочка символов получится, если к данной цепочке применить описанный алгоритм дважды (т.е. применить алгоритм к данной цепочке, а затем к результату вновь применить алгоритм)? алфавит:
:
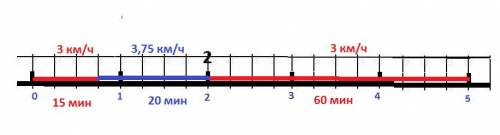
s=1.5 км - путь, который миша успел пройти за время t(1)=1 ч
v(1)=1.5 км/ч - скорость Миши за первый час пути (найдена по формуле v(1)=s/t(1))
Тогда время за которое Миша бы оставшуюся часть пути не меняя скорости будет равно: t(2)=(S-s)/v(1)
Отсюда получим время отправки автобуса, учитывая опоздание миши ( t(3)=20/60 ) :
t=t(1)+t(2)-t(3).
Теперь рассмотрим второй случай, когда миша приходит на станцию раньше, чем нужно ( t(4)=23/60 ):
Время за которое он пройдет оставшийся путь со скоростью v(2)=2 км/ч:
t(2')=(S-s)/v(2)
Отсюда t=t(1)+t(4)+t(2')
Приравниваем уравнения отправки автобуса:
t(1)+t(4)+t(2')=t(1)+t(2)-t(3);
t(4)+t(2')=t(2)-t(3);
t(4)+(S-s)/v(2)=(S-s)/v(1)-t(3)
(S-s)/v(1)-(S-s)/v(2)=t(3)+t(4)
((S-s)(v(2)-v(1))/v(1)v(2)=t(3)+t(4)
S=v(1)v(2)(t(3)+t(4))/(v(2)-v(1))+s
S=(1.5×2×43)/(60×0.5)+1.5=5.8 км