д)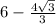 
Пошаговое объяснение:
Известно, что гипотенуза АС прямоугольного треугольника АВС равна 10 и ∠ВАС=60°.
Определим длины катетов АВ и ВС:
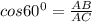
AB=AC·cosn60°=10·1/2=5,
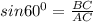
BC=AC·sins60°=10·√3/2=5√3.
Собака с поводком длиной 2 двигаясь по катетам АВ и ВС прямоугольного треугольника АВС может достичь (см. рисунок) все точки от А по N и от L по C.
Поэтому, чтобы определить длина части отрезка АС, то есть длину отрезка NL, до которой собака не может добраться определим длину отрезка АN и LC.
Так как ∠MAN=∠BAC, ∠AMN=∠ABC=90°, ∠ANM=∠ACB, то
треугольники ΔAMN и ΔABC подобны. Тогда из-за подобия треугольников ΔAMN и ΔABC:
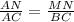или AN=AC·MN/BC=10·2/(5√3)=4/√3=4√3/3.
Также ∠LCK=∠ACB, ∠LKC=∠ABC=90°, ∠CLK=∠CAB, то
треугольники ΔLKC и ΔABC подобны. Тогда из-за подобия треугольников ΔLKC и ΔABC:
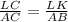или LC=AC·LK/AB=10·2/5=4.
Тогда длина части отрезка АС, до которой собака не может добраться
NL=AC-АN-LC=10-4√3/3-4=6-4√3/3.
д)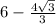
Пошаговое объяснение:
Известно, что гипотенуза АС прямоугольного треугольника АВС равна 10 и ∠ВАС=60°.
Определим длины катетов АВ и ВС:
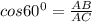
AB=AC·cosn60°=10·1/2=5,
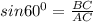
BC=AC·sins60°=10·√3/2=5√3.
Собака с поводком длиной 2 двигаясь по катетам АВ и ВС прямоугольного треугольника АВС может достичь (см. рисунок) все точки от А по N и от L по C.
Поэтому, чтобы определить длина части отрезка АС, то есть длину отрезка NL, до которой собака не может добраться определим длину отрезка АN и LC.
Так как ∠MAN=∠BAC, ∠AMN=∠ABC=90°, ∠ANM=∠ACB, то
треугольники ΔAMN и ΔABC подобны. Тогда из-за подобия треугольников ΔAMN и ΔABC:
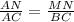или AN=AC·MN/BC=10·2/(5√3)=4/√3=4√3/3.
Также ∠LCK=∠ACB, ∠LKC=∠ABC=90°, ∠CLK=∠CAB, то
треугольники ΔLKC и ΔABC подобны. Тогда из-за подобия треугольников ΔLKC и ΔABC:
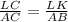или LC=AC·LK/AB=10·2/5=4.
Тогда длина части отрезка АС, до которой собака не может добраться
NL=AC-АN-LC=10-4√3/3-4=6-4√3/3.
Если рассматривать числа, больше 50, но меньше 100, то нас интересуют числа:
55,
60,
65,
70,
75,
80,
95.
Но известно также, что черепашек невозможно было построить по 2 в ряд. Значит, нам надо исключить все четные числа.
Остаются:
55,
65,
75,
85,
95.
Теперь надо исключить числа, которые делятся на 3 надо, поскольку по 3 в ряд также не получалось построить черепашек.
На 3 делятся числа, если сумма цифр, из которых состоит число, делится на 3.
55 (5+5=10) - не делится на 3;
65 (6+11=11) - не делится на 3;
75 (7+5=12) - делится на три;
85 (8+5=13) - не делится на 3;
95 (9+5=14) - не делится на 3.
Остаются числа:
55,
65,
85,
95.
Теперь рассмотрим числа, про которые можно сказать, что при делении на 4 в последнем ряду не хватает 1.
Для этого к числу прибавим недостающую и проверим, делится ли полученная сумма на 4 без остатка:
(55+1):4=56:6 = 14 - подходит!
(65+1):4=66:4 = 16 и 2 в остатке - не подходит
(85+1):4=86:4 = 21 и 2 в остатке - не подходит.
(95+1):4=96:4 = 24 - подходит!
Остались числа:
55,
95.
Теперь из этих двух выберем число, про которые можно сказать, что при делении на 3 в последнем ряду не хватает 1:
(55+1):3=56:3= 18 и 2 в остатке - не подходит.
(95+1):3=96:3=32 - подходит!
Значит искомое число 95.
ответ: 95.