Квадратным трёхчленом называется многочлен 2-ой степени, то есть выражение вида ax2 + bx + c, где a ≠ 0, b, c - (обычно заданные) действительные числа, называемые его коэффициентами, x - переменная величина.
Обратите внимание: коэффициент a может быть любым действительным числом, кроме нуля. Действительно, если a = 0, то ax2 + bx + c = 0·x2 + bx + c = 0 + bx + c = bx + c. В этом случае в выражении не остаётся квадрата, поэтому его нельзя считать квадратным трёхчленом. Однако, такие выражения-двучлены как, например, 3x2 − 2x или x2 + 5 можно рассматривать как квадратные трёхчлены, если дополнить их недостающими одночленами с нулевыми коэффициентами: 3x2 − 2x = 3x2 − 2x + 0 и x2 + 5 = x2 + 0x + 5.
Если стоит задача, определить значения переменной х, при которых квадратный трёхчлен принимает нулевые значения, т.е. ax2 + bx + c = 0, то имеем квадратное уравнение.
Если существуют действительные корни x1 и x2 некоторого квадратного уравнения, то соответствующий трёхчлен можно разложить на линейные множители: ax2 + bx + c = a(x − x1)(x − x2)
Замечание: Если квадратный трёхчлен рассматривать на множестве комплексных чисел С, которое, возможно, вы еще не изучали, то на линейные множители его можно разложить всегда.
Когда стоит другая задача, определить все значения, которые может принимать результат вычисления квадратного трёхчлена при различных значениях переменной х, т.е. определить y из выражения y = ax2 + bx + c, то имеем дело с квадратичной функцией.
При этом корни квадратного уравнения являются нулями квадратичной функции.
Квадратный трёхчлен также можно представить в виде
Средние вагоны поезда из 18 вагонов - это девятый и десятый.
Обозначим количество пассажиров в вагонах В₁, В₂,..., В₁₇, В₁₈.
В₁ + В₂ + В₃ + В₄ + В₅ = 199
В₂ + В₃ + В₄ + В₅ + В₆ = 199
В₃ + В₄ + В₅ + В₆ + В₇ = 199 и т.д.
Так как в 5 последовательных вагонах количество пассажиров постоянно, то убирая один вагон, добавить можно только вагон с таким же количеством пассажиров. Тогда
В₁ = В₆ = В₁₁ = В₁₆; В₂ = В₇ = В₁₂ = В₁₇; В₃ = В₈ = В₁₃ = В₁₈
В₄ = В₉ = В₁₄; В₅ = В₁₀ = В₁₅.
По условию
В₁ + В₂ + В₃ + ... + В₁₆ + В₁₇ + В₁₈ = 700 или
4В₆ + 4В₇ + 4В₈ + 3В₉ + 3В₁₀ = 700
4(В₆ + В₇ + В₈ + В₉ + В₁₀) - В₉ - В₁₀ =700
4 · 199 - В₉ - В₁₀ =700
796 - 700 = В₉ + В₁₀
В₉ + В₁₀ = 96
ответ : Д) 96
1. 151,9 см
2. 740 м
Пошаговое объяснение:
1. Длина окружности рассчитывается по формуле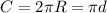
, где R - радиус, d - диаметр окружности. Подставим данные из условия получим: 
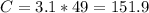см.
2. Масштаб карты 1:10000 означает, что на 1 см карты приходится 10 000 см на местности. Тогда на 7,4 см карты на местности будет приходиться 7,4 * 10 000 = 74000 см = 740 м = 0,74 км.