Відповідь:
12 коробок
Покрокове пояснення:
максимально возможное количество можно определить соотношением площадей дна ящика и коробки. Но в таком случае необходимо проверить, существует ли соответствующее размещение (задача в целых числах)
1) Определяем ширину дна ящика: 68 - 23 = 45 (см)
2) Определяем соотношение площадей: 68*45/17/15 = 4*3 = 12 (коробок)
3) Проверяем, существует ли размещение:
Действительно, 68 / 17 = 4 (целое число) и 45 / 15 = 3 (целое число). Можно разместить в 4 ряда по 3 коробки в каждом.
Решение: Запишем ОДЗ: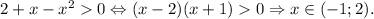 
Переходим к уравнению-следствию: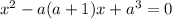 
.
Найдём дискриминант: ![D=[-a(a+1)]^2-4\cdot1\cdot a^3=a^4+2a^3+a^2-4a^3=a^4-2a^3+a^2=a^2(a^2-2a+1)=a^2(a-1)^2=[a(a-1)]^2.](/tpl/images/2005/6762/e07c3.png)
Дискриминант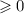 
при любых значениях параметра, а значит квадратное уравнение всегда имеет корень. При 
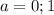дискриминант равен 0 и уравнение имеет единственное решение. Такой вариант нас не устраивает, поэтому будем рассматривать все 
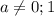. Для них квадратное уравнение имеет два корня:
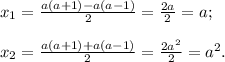
Чтобы исходное уравнение имело два корня необходимо, чтобы оба корня удовлетворяли ОДЗ, т.е.
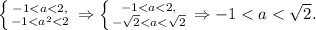
Не забудем исключить 0 и 1 из данного промежутка значений и получим окончательный ответ.
ОТВЕТ: при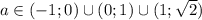 
.
1. Увеличится на 840.
2. Уменьшится на 595.
3. Увеличится на 765.
Пошаговое объяснение:
1. (a + 523) + (b + 317) = (a + b) + 523 + 317 = (a + b) + 840.
2. (a - 238) + (b - 357) = (a + b) - 238 - 357 = (a + b) - 595.
3. (a + 186) + (b + 256) + (c + 323) = (a + b + c) + 186 + 256 + 323 = (a + b + c) + 765.