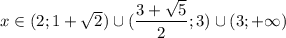-1
Пошаговое объяснение:
p(a) = a(10 - a) / (a - 5)
это означает, что если а = 0
p(0) = 0 (10 - 0) / (0 - 5) = 0
или если а = 1
p(1) = 1 (10 - 1) / (1 - 5) = -9/4 = -2.55
теперь, скажем, что а = 10 - а
p(10 - a) = (10 - a) (10 - (10 - a)) / (10 - a - 5) = (10 - a) * a / (5 - a) = a * (10 - a) / (5 - a)
посмотрим, что означает p(0) / p(1) = 0 / -2.55
по аналогии p(a) / p(10 - a) = (a(10 - a) / (a - 5)) / ( a * (10 - a) / (5 - a)) =
(a * (10 - a) * (5 - a)) / ((a - 5) * (10 - a) * a) = (5 - a) / (a - 5) = -1
Пошаговое объяснение:
ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть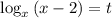 . Тогда
. Тогда 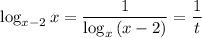 :
:
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
Первое неравенство имеет решение (с учётом ОДЗ)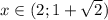
Второе неравенство раскладывается на множители:
Нули получившегося неравенства: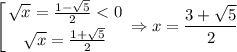
C учётом ОДЗ получаем, что в данном случае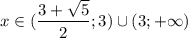 (левая граница меньше правой, так как √5 < 3).
(левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
Тогда промежутки не пересекаются, итоговый ответ: