Пошаговое объяснение:
в) (45-у)+18=58
(45-у)=58-18
45-у=40
у=45-40
У=5
Проверка
(45-5)+18=58
40+18=58
58=58
№ 4. x ≤ 0.75
№ 5. ( - ∞; - 1 ] ∪ [ 3; + ∞ )
Пошаговое объяснение:
№ 4. 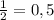
Тогда выражение имеет вид:
(0,5)^ (2*x) ≥ (0.125) ^ (1/2)
(0.5) ^ (2*x) ≥ ((0.5)^3)^(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3*(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3/2)
(0.5) ^ (2*x) ≥ (0.5) ^ 1.5
Т.к. 0,5 < 1, то имеем:
2 * х ≤ 1.5
x ≤ 1.5 / 2
x ≤ 0.75 или иначе записать можно так х ≤ 
№ 5. 7 ^ (x ^ 2) * 49 ^ ( - x) ≥ 343
7 ^ (x ^ 2) * 7^2^ ( - x) ≥ 7 ^ 3
7 ^ (x ^ 2) * 7^ ( - 2 * x) ≥ 7 ^ 3
7 ^ ((x ^ 2) + ( - 2 * x)) ≥ 7 ^ 3
7 ^ (x ^ 2 - 2 * x) ≥ 7 ^ 3
Т.к. 7 > 1, то запишем так:
x ^ 2 - 2 * x ≥ 3
Решим получившееся квадратное неравенство.
x ^ 2 - 2 * x = 3
x ^ 2 - 2 * x - 3 = 0
D = 16
x1,2 = (2±4)/2
x1 = 3 и x2 = -1
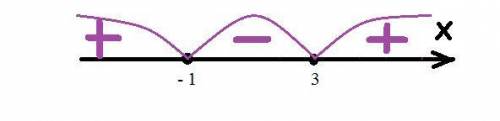
Решим методом интервалов.
( - ∞; - 1 ] ∪ [ 3; + ∞ )
Пусть n - количество золотых в кувшине. x - количество монет, которое должна была получить Алиса. y - количество монет, которое должен был получить Базилио. z - количество монет, которое должен был получить Буратино.
Составим уравнения по условию задачи.
Согласно плану Алисы: х = n/3, y = (n - n/3)/2 = n/3. Отсюда z = n - x - y = n - n/3 - n/3 = n/3
Согласно плану Базилио: y = n/2, x = (n - n/2)/3 = n/6. Отсюда z = n - n/2 - n/6 = 2n/6 = n/3
Следовательно, вне зависимости от того, какой план был выбран, Буратино получил n/3 (т.е. 5 - по условию) золотых. Значит n/3 = 5, откуда - n = 15.
ответ: 15 золотых.
у=-5
Пошаговое объяснение:
(45-у)+18=58
45+у+18=58
у=58-18-45
у=-5