I. (2sin²x - 7sinx + 3) · log₂ (x-8) = 0
ОДЗ : x-8 > 0; x > 8
Произведение равно нулю, когда один из множителей равен нулю.
1) 2sin²x - 7sinx + 3 = 0 - квадратное уравнение с неизвестным sinx
D = 7² - 4·2·3 = 25 = 5²
sin x = (7+5)/4 = 3 - не подходит под условие |sin x| ≤ 1
sin x = (7-5)/4 = 1/2
x₁ = π/6 + 2πn, n∈N, n≥2 ( ОДЗ: π/6 + 4π ≈ 13,1 > 8)
x₂ = 5π/6 + 2πk, k∈N ( ОДЗ: 5π/6 + 2π ≈ 8,9 > 8)
2) log₂ (x-8) = 0 ⇒ x - 8 = 2⁰
x = 1 + 8; x₃ = 9
==========================
II. x ∈ (3π; 6π)

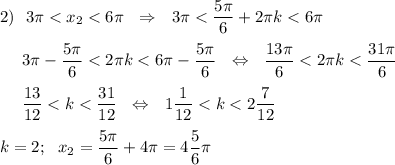
3) x₃ = 9 < 9,4 ≈ 3π - не входит в интервал
ответ:  ;
; 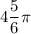
1. x = 6
x = -4
x = -5/8 или x = -0,625
2. x < -9
x > 1/2 или x > 0,5
x < 5
Пошаговое объяснение:
5 (x - 4) = x + 4
5x - 20 = x + 4
5x - x = 4 + 20
4x = 24
x = 6
5 (x + 1) = 2x - 7
5x + 5 = 2x - 7
5x - 2x = -7 - 5
3x = -12
x = -4
-3 (x + 5) = 5 (x - 2)
-3x - 15 = 5x - 10
-3x - 5x = -10 + 15
-8x = 5
x = -5/8 или x = -0,625
2. 6x - 5 (2x + 8) > 14 + 2x
6x - 10x - 40 > 14 + 2x
-4x - 40 > 14 + 2x
-4x - 2x > 14 + 40
-6x - 54 > 0 / * (-1)
6x + 54 < 0 / / 9
x + 9 < 0
x < -9
2x - 1 > 0
2x > 1
x > 1/2
15 - 3x > 0
3x < 15
x < 5