Полная колода карт (52 листа) разбивается наугад на две равные стопки по 26 листов. найти вероятность того, что в одной из стопок не будет ни одного туза. (введите ответ с точностью до трех знаков после запятой)
Из условия задачи следует, что ∠BMA = ∠CMK = 60◦ , а тогда и ∠AMK = 60◦. Далее можно рассуждать по-разному:
Первый Диагональ CA квадрата является биссектрисой внутреннего угла треугольника CMK, а луч MA — биссектрисой его внешнего угла, поэтому вершина A — центр вневписанной окружности этого треугольника. Следовательно, KA также является биссектрисой внешнего угла треугольника CMK, поэтому ∠AKD = 1 2 ∠MKD = 75◦ .
Второй Продлим отрезок KM до пересечения с прямой AB в точке P. Тогда ∠PMB = ∠CMK = ∠AMB. Следовательно, прямоугольный треугольники PMB и AMB равны (по катету и острому углу), тогда PB = AB, то есть AP = 2a, где a — сторона данного квадрата, и PM = AM. По свойству катета, противолежащего углу в 30◦ в прямоугольном треугольнике, AM = 2BM и MK = 2MC. Следовательно, PK = PM + MK = 2(BM + MC) = 2BC = 2a. Таким образом, треугольник APK — равнобедренный с углом 30◦ при вершине P, поэтому его угол при основании равен 75◦ . Так как ∠MKD = 150◦ , а ∠MKA = 75◦ , то ∠AKD = 75◦ .
Из условия задачи следует, что ∠BMA = ∠CMK = 60◦ , а тогда и ∠AMK = 60◦. Далее можно рассуждать по-разному:
Первый Диагональ CA квадрата является биссектрисой внутреннего угла треугольника CMK, а луч MA — биссектрисой его внешнего угла, поэтому вершина A — центр вневписанной окружности этого треугольника. Следовательно, KA также является биссектрисой внешнего угла треугольника CMK, поэтому ∠AKD = 1 2 ∠MKD = 75◦ .
Второй Продлим отрезок KM до пересечения с прямой AB в точке P. Тогда ∠PMB = ∠CMK = ∠AMB. Следовательно, прямоугольный треугольники PMB и AMB равны (по катету и острому углу), тогда PB = AB, то есть AP = 2a, где a — сторона данного квадрата, и PM = AM. По свойству катета, противолежащего углу в 30◦ в прямоугольном треугольнике, AM = 2BM и MK = 2MC. Следовательно, PK = PM + MK = 2(BM + MC) = 2BC = 2a. Таким образом, треугольник APK — равнобедренный с углом 30◦ при вершине P, поэтому его угол при основании равен 75◦ . Так как ∠MKD = 150◦ , а ∠MKA = 75◦ , то ∠AKD = 75◦ .
Количество всевозможных исходов: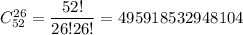
В одной из стопок может быть 4 туза или нет, т.е. в первой стопке - 4 туза, а в другой нет тузов или наоборот. Таких вариантов 2.
Выбрать четыре туза можно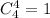
оставшиеся карты без тузов 
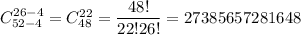. Всего таких
Искомая вероятность:
ответ: 0,110.