Пошаговое объяснение:
В первом среднее арефмитическое 6. Потомучто мы 9+7+4+6+3+7=36 и разделить на 6 будет 6.
1) My favourite weather is rainy.
Моя любимая погода - это дождливая погода.
2) We are at the hotel because of the storm.
Из-за шторма мы находимся в отеле(гостинице).
3) Is it spring or summer in your photo?
Это весна или лето на твоей фотографии?
4)The weather is not snowy.
Погода не снежная.
1) б)
2) а)
3) г)
4) в)
Объяснение:
1) б) т.к это время Present Simple
2) а) т.к. это время Past Simple
3) г) т.к. это время Past Simple и was это будет сказуемым
4) в) т.к. это время Present Simple
Пошаговое объяснение:
6:2=3 - коэффициент подобия
9:3=3 - В1С1
12:3=4 - А1С1
Чтобы найти сколькими нулями оканчивается произведение нужно найти сколько раз в этом произведении встречается множитель 10.
Заметим, что 10 раскладывается на простые множители как 10=2·5. Очевидно, сомножителей "2" будет больше чем сомножителей "5". Таким образом, нужно узнать число множителей "5" в произведении. Каждый такой множитель в паре с множителем "2" даст множитель "10" и соответственно дополнительный ноль на конце числа.
Найдем, сколько чисел содержит множитель "5". Всего среди первых 2020 натуральных чисел таких чисел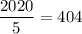 
, но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
Но некоторые числа содержат не один множитель "5", а два. Найдем количество таких чисел.
Для этого разделим 2020 на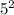 
:
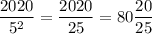
Значит, последнее число, которое содержит в своем составе два множителя "5" - это число 
. Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
Еще некоторые числа содержат три множителя "5". Найдем количество таких чисел. Для этого разделим 2020 на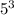 
:
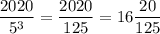
Значит, последнее число, которое содержит в своем составе три множителя "5" - это число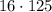 
. Первое такое число - 125. Значит, всего таких чисел 16.
И, наконец, некоторые числа содержат сразу четыре множителя "5". Найдем их количество. Для этого разделим 2020 на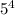 
:
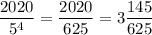
Значит, последнее число, которое содержит в своем составе четыре множителя "5" - это число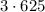 
. Первое такое число - 625. Значит, всего таких чисел 3.
Чисел, кратных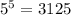 
среди множителей нет.
Итак, 401 число содержат в своем составе множитель "5", 80 чисел содержат второй множитель "5", 16 чисел содержит третий множитель "5" и 3 числа содержат четвертый множитель "5". Значит, всего множителей "5" имеется:
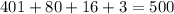
Значит, число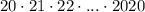 
оканчивается 500 нулями.
ответ: 500
Чтобы найти сколькими нулями оканчивается произведение нужно найти сколько раз в этом произведении встречается множитель 10.
Заметим, что 10 раскладывается на простые множители как 10=2·5. Очевидно, сомножителей "2" будет больше чем сомножителей "5". Таким образом, нужно узнать число множителей "5" в произведении. Каждый такой множитель в паре с множителем "2" даст множитель "10" и соответственно дополнительный ноль на конце числа.
Найдем, сколько чисел содержит множитель "5". Всего среди первых 2020 натуральных чисел таких чисел 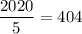, но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
Но некоторые числа содержат не один множитель "5", а два. Найдем количество таких чисел.
Для этого разделим 2020 на :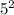
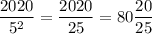
Значит, последнее число, которое содержит в своем составе два множителя "5" - это число . Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
Еще некоторые числа содержат три множителя "5". Найдем количество таких чисел. Для этого разделим 2020 на :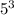
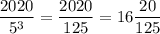
Значит, последнее число, которое содержит в своем составе три множителя "5" - это число 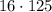. Первое такое число - 125. Значит, всего таких чисел 16.
И, наконец, некоторые числа содержат сразу четыре множителя "5". Найдем их количество. Для этого разделим 2020 на :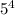
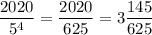
Значит, последнее число, которое содержит в своем составе четыре множителя "5" - это число 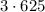. Первое такое число - 625. Значит, всего таких чисел 3.
Чисел, кратных 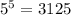среди множителей нет.
Итак, 401 число содержат в своем составе множитель "5", 80 чисел содержат второй множитель "5", 16 чисел содержит третий множитель "5" и 3 числа содержат четвертый множитель "5". Значит, всего множителей "5" имеется:
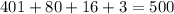
Значит, число 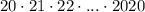оканчивается 500 нулями.
ответ: 500
Среднее арифметическое:
1) 6
2) 3.7
3) 0.52
Медиана:
1) 6.5
2) 3.8
3) 1/2
Размах:
1) 6
2) 4
3) 0.5