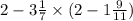
Сначала для удобства переведём дроби в неправильные:
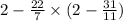
Теперь поочерёдно начнём выполнять действия. Первым действием является скобка. Перед тем, как выполнить вычитание, нужно привести оба числа в одинаковому знаменателю, для этого умножим 2 на 11 и после этого вычтем:
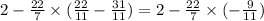
Следующим действием является умножение. Обе дроби являются отрицательными, значит их произведение будет положительным, так как при умножении минуса на минус бужет плюс. Сократим и умножим:
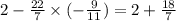
Осталось выполнить последнее действие, которым является сложение. Для начала приведём эти числа к общему знаменателю, сложим и выделим целую часть:
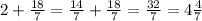
Вот и ответ.
7x-1(3+2x)=x+9
7x−1(3+2x)=x+9
Вычисление значения
1
Переставьте члены уравнения
7
−
1
(
3
+
2
)
=
+
9
7
−
1
(
2
+
3
)
=
+
9
2
Раскройте скобки
7
−
1
(
2
+
3
)
=
+
9
7
−
2
−
3
=
+
9
3
Объедините подобные члены
7
−
2
−
3
=
+
9
5
−
3
=
+
9
4
Прибавьте
3
3
3
к обеим частям уравнения
5
−
3
=
+
9
5
−
3
+
3
=
+
9
+
3
5
Упростите
Сложите числа
Сложите числа
5
=
+
1
2
6
Вычтите
x
x
из обеих частей уравнения
5
=
+
1
2
5
−
=
+
1
2
−
7
Упростите
Объедините подобные члены
Объедините подобные члены
4
=
1
2
8
Разделите обе части уравнения на один и тот же член
4
=
1
2
4
4
=
1
2
4
9
Упростите
Сократите числитель и знаменатель
Разделите числа
=
3
Решение
=
3
Пошаговое объяснение:
∠2 = 50°, ∠1 = 130°.
Пошаговое объяснение:
1. ∠1 = ∠3 (вертикальные).
2. ∠3 + ∠2 = 180° как внутренние односторонние при k ll d и секущей l, тогда и
∠1 + ∠2 = 180°.
3. Пусть ∠2 = х°, тогда по условию ∠1 = 2 3/5•х.
Зная, что ∠1 + ∠2 = 180°, составим и решим уравнение:
х + 2 3/5х = 180
3 3/5х = 180
х = 180 : 3 3/5
х = 180•5/18
х = 10•5
х = 50
∠2 = 50°, тогда по условию ∠1 = 2 3/5•50° = 130°.