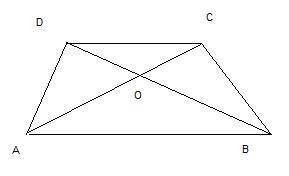
1. Треугольники DOC и АОВ подобны по первому признаку подобия треугольников: два угла одного треугольника соответственно равны двум углам другого. В нашем случае углы DOC и АОВ равны как вертикальные углы, а углы DCA и САВ равны как накрест лежащие углы при пересечении параллельных прямых DC и АВ секущей АС.
2. Выразим ОС как 15-АО
3. Поскольку треугольники подобны, можно записать:
АО / ОС = АВ / DC,
АО = ОС*АВ / DC
AO = (15-AO)*AB / DC
AO = (15-AO)*96 / 24
24AO = (15-AO)*96
24AO = 1440 - 96AO
120AO = 1440
AO = 12 см
Объяснение:
3n - 4, 4n - 5, 5n - 3 - простые n ∈ N
простые 2, 3, 5, 7, 11, 13
одно четное простое число 2
n ≥ 2 ( 3n - 4 < 0 при n = 1)
пусть n - нечетное, тогда
(3*нечетное - 4) - нечетное
(4*нечетное - 5) - нечетное
(5*нечетное - 3) - четное
5n - 3 = 2
5n = 5
n = 1
но такого не может быть n ≥ 2
пусть n - четное, тогда
(3*четное - 4) - четное
(4*четное - 5) - нечетное
(5*четное - 3) - нечетное
3n - 4 = 2
3n = 6
n = 2
подходит, но надо проверить два оставшихся
4n - 5 = 4*2 - 5 = 3 простое
5n - 3 = 5*2 - 3 = 7 простое
3n - 4 = 3*2 - 4 = 2 простое
да только при n = 2 числа простые