а) 3b + 2c > 0
б) > 0
Два выражения больше нуля!
Z - это множество целых чисел
m² - 10 * m + 27 (m - 5)² + 2 2
= = m - 5 +
m - 5 m - 5 m - 5
Значение дроби будет целым, если 2 делится нацело на m - 5
Это возможно, если m - 5 = ± 1, ± 2 или m = 3, 4, 6, 7
При m = 3 дробь равна 3 - 5 + 2 / (-2) = -2 - 1 = -3
При m = 4 дробь равна 4 - 5 + 2 / (-1) = -1 - 2 = -3
При m = 6 дробь равна 6 - 5 + 2 / 1 = 1 + 2 = 3
При m = 7 дробь равна 7 - 5 + 2 / 2 = 2 + 1 = 3
Итак, множество целых значений дроби при целых значениях аргумента сосавляют 2 числа: -3 и 3
1) 5=-1-(3-9x)
5=-1-3+9х
5=-4+9х
-4+9х=5
9х=5+4
9х=9
х=9/9
х=1
5=-1-(3-9)
5=5
2) 9-(8x-11)=12
9-8х+11=12
20-8х=12
20-12=8х
8х=8
х=8/8
х=1
9-(8-11)=12
12=12
3) (6x+1)-(3-2x)=14
6х+1-3+2х=14
8х-2=14
8х=14+2
8х=16
х=16/8
х=2
(6*2+1)-(3-2*2)=14
(12+1)-(3-4)=14
14=14
4) 12=(7x-9)-(11-x)
12=7х-9-11+х
12=8х-20
8х-20=12
8х=12+20
8х=32
х=32/8
х=4
12=(7*4-9)-(11-4)
12=(28-9)-7
12=12
5) (10x-3)+(14x-4)=8-(15-22x)
10х-3+14х-4=8-15+22х
10х+14х-22х=8-15+3+4
2х=0
х=0
(10*0-3)+(14*0-4)=8-(15-22*0)
-3-4=8-15
-7=-7
6)(2x+3)+(3x+4)+(5x+5)=12-7x
2х+3+3х+4+5х+5=12-7х
2х+3х+5х+7х=12-3-4-5
17х=0
х=0
(2*0+3)+(3*0+4)+(5*0+5)=12-7*0
3+4+5=12
12=12
a) 3b+2c>0
б)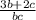 >0
>0
Объяснение: