а) 0.125 м/с
б) 0.875 м/с
в) 0.5 м/с
Объяснение:
Скорость равна отношению пройденного пути ко времени, которое ушло на прохождение этого пути.
a) в течение первых 4 секунд путь изменился с 2 до 2.5 м, то есть на 0.5 метров. Пройденный путь = 0.5м, время на это ушло 4с -значит скорость = 0.5/4=0.125 м/с
б) в течении последних 4 секунд путь изменился с 2.5 до 6 м, то есть на 6-2.5=3.5 метров. Пройденный путь = 3.5м, время на это ушло 4с -значит скорость = 3.5/4=0.875 м/с
в) в течении всех 8 секунд путь изменился с 2 до 6 м, то есть на 4 метра. Пройденный путь = 4м, время на это ушло 8с -значит скорость = 4/8=0.5 м/с
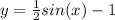
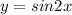
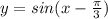

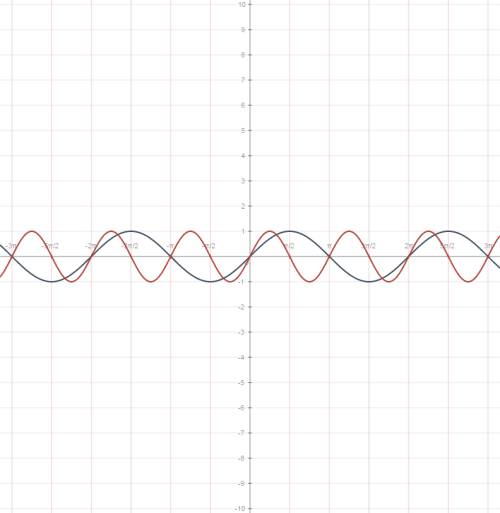
Объяснение:
Найдем производную и приравняем к 0.
g'(x) = 13*3x^2 + 2(a+2)x + (a^2+4a-12) = 0
D/4 = (a+2)^2 - 39(a^2+4a-12) = a^2+4a+4-39a^2-156a+468
D/4 = -38a^2 - 152a + 472 > 0
38a^2 + 152a - 472 < 0
19a^2 + 76a - 236 < 0
D/4 = 38^2 + 19*236 = 5928
a1 = (-38 - √5928)/19 ≈ -6,05
a2 = (-38 + √5928)/19 ≈ 2,05
Нам нужно, чтобы было x1 >= -2; x2 <= 9
x1 = [-a-2 - √(-38a^2-152a+472)]/39 >= -2
x2 = [-a-2 + √(-38a^2-152a+472)]/39 <= 9
Осталось решить эти два неравенства, с учётом области определения
а € ((-38-√5928)/19; (-38+√5928)/19)