![1)\; \; y=3x-2\; \; ,\; \; \; x\in D(y)=(-\infty ,+\infty )\\\\2)\; \; y=4-x^2\; \; ,\; \; \; x\in D(y)=(-\infty ,+\infty )\\\\3)\; \; y=-2,5\; \; ,\; \; \; x\in D(y)=(-\infty ,+\infty )\\\\4)\; \; y=\frac{5}{x\, (x-3)}\\\\x\ne 0\; \; ,\; \; x\ne 3\; \; ,\; \; \; x\in D(y)=(-\infty ,0)\cup (0,3)\cup (3,+\infty )\\\\5)\; \; y=\sqrt{2x-4}\\\\2x-4\geq 0\; ,\; \; x\geq 2\; \; ,\; \; \; x\in D(y)=[\, 2;+\infty )\\\\6)\; \; y=\frac{1}{x}\sqrt{5-2x}\; \; ,\\\\\left \{ {{x\ne 0} \atop {5-2x\geq 0}} \right. \left \{ {{x\ne 0} \atop {x\leq 2,5}} \right.\\\\x\in D(y)=(-\infty ,0)\cup (0\, ;\, 2,5\, ]](/tpl/images/1014/7714/c8d28.png)
Відповідь: a) x ∈ R або х ∈ (-∞; +∞)
б) x ∈ R або х ∈ (-∞; +∞)
в) x ∈ R або х ∈ (-∞; +∞)
г) 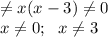
х ∈ (-∞; 0)∪(0;3)∪(3;+∞)
г) 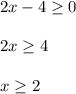
х ∈ [2; +∞)
д) 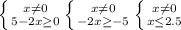
х ∈ (-∞; 0)∪(0;2.5]
Пояснення:
4ab+5b²;
при a=1; b=⅕ ответ: 1
Объяснение:
(a + 2b)²- (a - b)(b + a) = a²+ 4ab + 4b² - (a²- b²) = a² + 4ab + 4b² - a² +b²
взаимоуничтожаем a² и -a², приводим подобные члены и получаем: 4ab+5b²
при a=1; b=⅕ 4ab+5b²= 4×1×0,2 + 5×0,2² = 0,8 + 0,2 = 1
В выражении присутствуют формулы квадрат суммы и разность квадратов, раскрываем скобки, с учётом знаков перед скобкой, в данном случае "-", следовательно, все знаки внутри скобок меняем на противоположные. Потом взаимоуничтожаем a² и -a², приводим подобные члены и получаем 4ab+5b². Далее находим значение выражения 4ab+5b², при установленных значениях, для этого подставляем числа в полученное выражение и решаем.