#1. |2x-3|=3-2x, если х<3/2; |2x-3|=2x-3, если х≥3/2;
|x-2|=2-x, если х<2; |x-2|=-2x, если х≥2;
|x-6|=6-x, если х<6; |x-6|=x-6, если х≥6.
Получаем три случая:
1) на множестве (-∞;3/2)U[2;6) получаем неравенство
(2х-3)(х-2)≥(6-х)+2
2х²-3х-4х+6-6+х-2≥0
2х²-6х-2≥0
х²-3х-1≥0
D=9+4=13
![(x-\frac{3-\sqrt{13}}{2})(x-\frac{3+\sqrt{13}}{2})\geq0 \\\ x \in (-\infty; \frac{3-\sqrt{13}}{2}] \cup [\frac{3+\sqrt{13}}{2}; +\infty)](/tpl/images/0172/7524/775a9.png)
C учётом (-∞;3/2)U[2;6) получим ![x \in (-\infty; \frac{3-\sqrt{13}}{2}]](/tpl/images/0172/7524/fc8b3.png)
2) на интервале 1,5≤х<2 получим неравенство
(2х-3)(2-х)≥(6-х)+2
4х-6-2х²+3х-6+х-2≥0
-2х²+8х-14≥0
х²-4х+7≤0
D=16-28<0
решений нет
3) на интервале х≥6 получим неравенство
(2х-3)(х-2)≥(х-6)+2
2х²-3х-4х+6+6-х-2≥0
2х²-8х+10≥0
х²-4х+5≥0
D=16-20<0
решений нет
ответ:
#2. Пусть ∆АВС-прямоугольный треугольник с гипотенузой АВ, катетами АС и ВС.
По условию ВС+АВ=11, tg В = 3/4.
По определению тангенса острого угла прямоугольного треугольника
tg B=AC/BC=3/4 => 3BC=4AC =>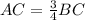 
По теореме Пифагора АВ² = АС² + ВС²
Пусть ВС=х, тогда АВ=11-х, АС=3х/4
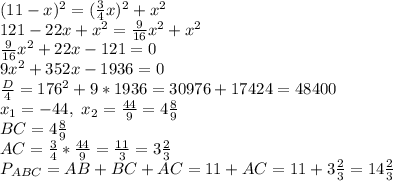
ответ: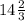 
ответ: 180
Объяснение:
Мы знаем что данное трехзначное число в 20 раз больше его суммы цифр , это значит что оно делится на 20, а значит неизбежно кончается цифрой 0 , а предпоследняя его цифра должна быть четной.
Так же можно приметить такое свойство , что любое число дает тот же остаток от деления на 9 , что и его сумма цифр.
Пусть остаток от деления на 9 его суммы цифр равен p (S=9*n+p) , тогда наше число : N=20*S=9*n*20+20*p. (S-сумма цифр)
Таким образом 20*p при делении на 9 так же дает остаток p.
20*p=9*k+p
19*p=9*k
тк 19- простое число , то p делится на 9.
тк p=( 0,1,2,3...8) , то единственное p удовлетворяющее этому условию:
p=0 , другими словами такое трехзначное число должно делится на 9.
Последняя цифра 0 , а максимальная сумма двух цифр с одной четной цифрой : 8+9=17<18=2*9 .
А значит нужно искать такие цифры , чтобы их сумма была равна 9. ( тк сумма цифр должна делится на 9)
Но если сумма цифр 9 , то само число : 9*20=180
Проверим : 1+8+0=9 , верно.
Таким образом единственное трехзначное число , что удовлетворяет этому условие является : 180
13м
Объяснение:
Так как высота 3м давала тень 1,5м,а точнее половину то тогда если тень ровна 6,5м значит столд равен 13м