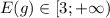В решении.
Объяснение:
По заданному графику определите:
а) область определения функции;
Область определения - это значения х, при которых функция существует. Обозначение D(f) или D(у).
Согласно графика, данная функция существует от х= -5 до х=6.
Кружок у х= -5 закрашен, значит, точка принадлежит числовому промежутку, скобка квадратная.
Кружок у х=6 не закрашен, точка не принадлежит числовому промежутку, скобка круглая.
Область определения функции:
D(f) = х∈[-5; 6).
б) область значений функции;
Область значений функции - это проекция графика на ось Оу. Обозначение Е(f) или Е(у).
Согласно графика, самое меньшее (самое "низкое") значение у= -1, самое большее (самое "высокое") у=5.
Область значений функции:
Е(f) = [-1; 5].
в) значения аргумента, при которых функция равна нулю;
График пересекает ось Ох в двух точках, в этих точках у=0.
у=0 при х=0 и х=1.
г) промежутки возрастания;
Функция возрастает в промежутке при х от -4 до -2 и при х от 0,5 до 6.
Запись: f(x) возрастает при х∈(-4; -2); при х∈(0,5; 6).
д) промежутки убывания.
Функция убывает при х от -5 до -4 и при х от -2 до 0,5.
Запись: f(x) убывает при х∈(-5; -4); при х∈(-2; 0,5).
a)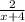 
b) 
Объяснение:
Будем раскладывать на множиели при этой формулы :
ax² + bx +c = a(x - x₁)(x - x₂)
a) Для начала нам потребуется найти корни :
x² - x -20 = 0
{ x₁ + x₂ = 1 (система)
{ x₁ × x₂ = -20
x₁ = - 4
x₂ = 5
⇒ x² - x -20 = 1(x - (-4))(x - 5) = (x+4)(x-5)
Теперь подставляем это выражение в знаменатель, а также раскладываем на множители числитель :
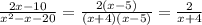
b) Так же, как и в примере, нам нужно найти корни, но уже двух многочленов : (x²+12x+27) и (x²+8x-9).
x² + 12x + 27 = 0
Буду решать через выделение полного квадрата :
(x + 6)² - 9 = 0
(x + 6)² = 9
x+6 = -3 x+6 = 3
x₁ = -9 x₂ = -3
⇒ x² + 12x + 27 = 1(x - (-9))(x - (-3)) = (x+9)(x+3)
Теперь разложим многочлен на множители, который в знаменателе :
x² + 8x - 9 = 0
Решаю опять же через выделение полного квадрата :
(x + 4)² - 25 = 0
(x + 4)² = 25
x+4 = -5 x+4 = 5
x₁ = -9 x₂ = 1
⇒ x² + 8x - 9 = 1(x - (-9))(x - 1) = (x+9)(x-1)
Теперь подставляем эти два выражения :
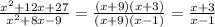
Найдём дискриминант трёхчлена под корнем:
Дискриминант отрицателен, коэффициент при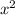
положителен, а значит, область определения функции 
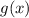равна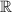 
(ведь под корнем должны быть только положительные числа).
Найдём минимальное значение многочлена под корнем с производной — обозначим его как функцию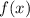
:
Тогда минимальное значение исходной функции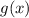
будет равно 
.
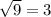Из той же формулы производной видно, что функция под корнем неограниченно возрастает при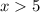
. Это значит, что функция 
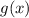не имеет максимального значения.
ответ: