a2 = a1 + d = - 6 => a3 - a2 = a1 + 2d - a1 - d = -4 => d =4
a3 = a1 + 2d = - 2
a2 = a1 + d = -6 => a1 = a2 - d = -6 - 4 = -10
a15 = a1 + 14d = -10 + 56 = 46
Давай я попробую тебе сначала объяснить как делать Б,
Чтобы решать такие задания, тебе необходимо знать формулы сокращённого умножения, и формулу нахождения дискриминанта.
1) (a + b)² = a² + 2ab + b²
2) (a – b)² = a² – 2ab + b²
3 ) (a + b)(a – b) = a² – b²
А теперь перейдем к примеру:
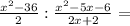
и видим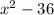 
это ни что иное, как формула под номером 3 (разность квадратов, расписываем ее (х-6)(х+6)
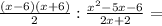
Все мы знаем, что при делении 1 дроби на 2, необходимо вторую перевернуть, так мы переходим к умножению
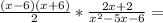
2х+2 тут тоже все просто , выносим 2 за скобку , и получаем 2*(х+1)
осталось перейти к самому сложно, и кстати если вы заметили
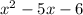(это задание под пунктом А)
Когда видишь что-то похожее на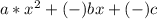 
, где а, b,c цифры, значит тебе нужно искать дискриминант.
Д= b² -4 a c = 25-4*1*(-6) = 49= 7²
x₁=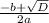 
=( 5+7)/2 = 6
x₂ = 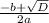= (5-7)/2= -1
это все записывается потом так (х-6) (х+1) ( тоже формула)
наше уравнение теперь выглядит так:
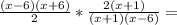( осталось только сократить все ) = х+6 .
ответ: x+6
теперь перейдем к уравнению А, учитывая, что мы почти его сделали.
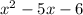= 0
Д= b² -4 a c = 25-4*1*(-6) = 49= 7²
x₁= 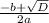=( 5+7)/2 = 6
x₂ = 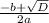= (5-7)/2= -1
(х-6) (х+1)=0
Допустимые значения:
x-6=0 x+1=0
x=6 x=-1
ответ: (- ∞; - 1] ; [-1;6]; [6; +∞)
В решении.
Объяснение:
Побудуйте графік функції y=x²-4x-5. Користуючись графіком, знайдіть:
1) Найменше значення функції;
2) Множину розв'язків нерівності x²-4x-5>0;
3) Проміжок, на якому функція y=x²-4x-5 зростає.
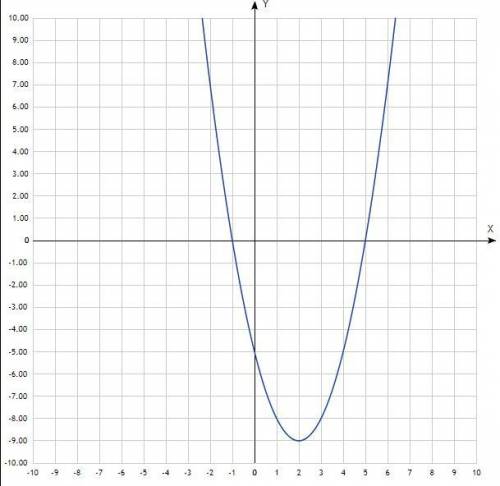
Постройте график функции y = x² - 4x - 5.
Пользуясь графиком, найдите:
1) Наименьшее значение функции;
2) Множество решений неравенства x²- 4x - 5 > 0;
3) Промежуток, на котором функция y = x² - 4x - 5 возрастает.
Придать значения х, подставить в уравнение, вычислить значения у, записать в таблицу, построить по точкам график.
График квадратичной функции, парабола со смещённым центром, ветви направлены вверх.
Таблица:
х -2 -1 0 1 2 3 4 5 6
у 7 0 -5 -8 -9 -8 -5 0 7
1) Наименьшее значение функции определяется ординатой её вершины. Согласно графика, наименьшее значение у = -9.
2) x²- 4x - 5 > 0;
Приравнять к нулю:
x²- 4x - 5 = 0
Уравнение квадратичной функции, ветви направлены вверх, пересекают ось Ох при х = -1 и х = 5.
Решение неравенства: х∈(-∞; -1)∪(5; +∞).
Неравенство строгое, скобки круглые.
3) Функция возрастает при х∈(2; +∞).
На промежутке от х = 2 до + бесконечности.
d=a3-a2=-2-(6)=4
a1=a2-d=-6-4=-10
a15=a1+14d=-10+14*4=46