Question

При делении многочлена p(x)=x³-ax²+bx-1 поочередно на q1(x)=x, q2(x)=x+1, q3(x)=x-2 получается один и тот же остаток. найдите остаток от деления p(x) на q(x)= x²-3
, 50 !

Answer 1

По теореме Безу

P₁(0) = 0³ - a · 0² + b · 0 - 1 = -1

P₂(-1) = (-1)³ - a · (-1)² + b · (-1) - 1 = -1 - a - b - 1 = -a - b - 2

P₃(2) = 2³ - a · 2² + b · 2 - 1 = 8 - 4a + 2b - 1 = 2b - 4a + 7

Составим систему уравнений, по условию

$\displaystyle\left \{ {{-a-b-2=-1} \atop {2b-4a+7=-1}} \right.~~~\Rightarrow~~~~\left \{ {{a+b=-1} \atop {b-2a=-4}} \right.$

От первого уравнения отнимем второе уравнение, получим

a + b - b + 2a = -1 + 4

3a = 3

a = 1

b = -1 - a = -2

Таким образом,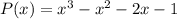 $P(x)=x^3-x^2-2x-1$. Поделив в столбик многочлен P(x) на двучлен Q(x) = x² - 4, получим остаток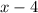 $x-4$

ответ: x - 4.