Объяснение:
1 √54 < x < √124
54< x²< 124
смотрим какие квадраты в промежутке
64, 81, 100, 121
8, 9, 10, 11
2 √125-√64 = 5√5-8
3 √(18-2х) при х=-9 ⇒ √36 = 6
4 Z - множество целых чисел, -127 целое, верно
5 Z - множество целых чисел, 346,3 не целое, неверно
6 Q - рациональные π иррациональное число. неверно
7 √23-√22 >0 т. к. 23>22
т. е. допустим что √23-√22 >0 ⇒ √23> √22 возведем обе части в квадрат 23 >22 да! √23-√22 >0
8 пусть – √34 < - √33 ⇒ умножим обе части на -1 ⇒ √34 >√33 - в квадрат ⇒ 34 >33 да – √34 < - √33
9 √124 < x < √245
124 <x²< 245
x² 144 169 196 225
x = 12, 13, 14, 15
Перенесем все влево и вынесем за скобки :
:
Из этого следует, что уравнение всегда имеет хотя бы одно решение - . Задача сводится к тому, чтобы посмотреть, при каких
. Задача сводится к тому, чтобы посмотреть, при каких  будут корни у уравнения
будут корни у уравнения  и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
1) проверим, при каком значении корнем уравнения
корнем уравнения  будет
будет  . Подставляем ноль в уравнение:
. Подставляем ноль в уравнение: 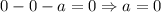 . При
. При  имеем:
имеем:
Делаем вывод, что при уравнение имеет два корня:
уравнение имеет два корня: 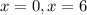 .
.
2) при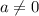 уравнение
уравнение  не может иметь корень
не может иметь корень  . Уравнение - квадратное. Сразу ищем дискриминант:
. Уравнение - квадратное. Сразу ищем дискриминант: 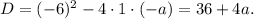
Здесь рассматриваем 3 случая:
2.1. Если , то уравнение
, то уравнение  решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
2.2. Если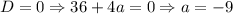 , то подставляя вместо параметра -9 в итоге получаем:
, то подставляя вместо параметра -9 в итоге получаем: 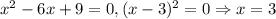 . Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
. Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
2.3. Если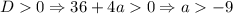 , то уравнение
, то уравнение  имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит
имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит  , а мы его проверяли отдельно - при
, а мы его проверяли отдельно - при  корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
ОТВЕТ: При уравнение имеет единственный корень; при
уравнение имеет единственный корень; при 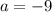 и
и  уравнение имеет два различных корня; при
уравнение имеет два различных корня; при 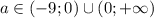 уравнение имеет три различных корня.
уравнение имеет три различных корня.