Значение выражения
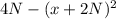
наибольшее при значении

При
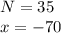
значение выражения равно
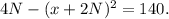
Объяснение:
Обозначим за a значение выражения, данное в условии:
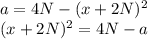
Для любых значений х и N левая часть равенства не может быть отрицательной, т.к. в ней выражение возведено в квадрат.
Соответственно, правая часть равенства тоже должна быть более или равна нулю:
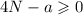
Отсюда можно выразить искомое а
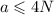
Соответственно, максимальное значение, которое может принять наше выражение, равно 4N
(по сути, это значение выражения, когда под квадратом ноль)
Подставим 4N в начальную формулу
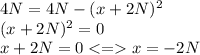
При значениях N = 35 получаем
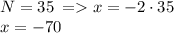
А значение выражения равно:
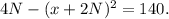
ответ:1) Задание
Дана функция
найти промежутки возрастания и убывания
По признаку возрастания и убывания функции на интервале:
если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;
если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Найдем производную данной функции
найдем точки экстремума, точки в которых производная равна нулю
отметим точки на числовой прямой и проверим знак производной на промежутках
___+-+__
0 2
Значит на промежутках (-оо;0) ∪ (2;+оо) функция возрастает
на промежутке (0;2) функция убывает
точки х=0 точка минимума, х=2 точка максимума
Найти наибольшее и наименьшее значение функции на отрезке [-2; 1].
Заметим, что х=2 точка максимума не входит в данный промежуток,
а х=0 принадлежит данному промежутку
Проверим значение функции в точке х=0 и на концах отрезка
Значит наибольшее значение функции на отрезке [-2;1]
в точке х=0 и у(0)=1
значит наименьшее значение функции на отрезке [-2;1]
в точке х=-2 и у(-2)= -19
2. Напишите уравнение к касательной к графику функции
f(x)=x^3-3x^2+2x+4 в точке с абсциссой x0=1.
Уравнение касательной имеет вид
найдем производную данной функции
найдем значение функции и производной в точке х=1
подставим значения в уравнение касательной
Объяснение:
x∈(-∞;-5)U[0.75;+∞)
Объяснение:
решаем методом интервалов
нули функции : -5 ; 3/4
+++++(-5)------[3/4]++++++
ответ: x∈(-∞;-5)U[3/4;+∞)