Задание №1.
1. На березе растут яблоки - Невозможное.
2. При бросании игральной кости выпала цифра 6 - Равновозможное.
3. За летом наступает осень - Достоверное.
Задание №2.
Всего двухзначных чисел у нас - 90 (от 10 до 99). Проще всего рещать в лоб, выбирая подходящие числа:
1) Нулём оканчивается каждое десятое из них, т.е. всего таких чисел 9. P = 9/90=0,1
2) Из одинаковых цифр состоит каждое одиннадцатое из них, начиная с 11, т.е. всего таких чисел 9. P = 9/90=0,1
3) Больше 27 и меньще 46 - всего 18 чисел, т.е. P =18/90=0,2
4) Квадратами целого числа являются 16, 25, 36, 49, 64, 81 - итого 6. P = 6/90=1/15
Задание №3.
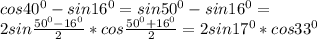
Объяснение:
Объяснение: ОДЗ:
{х + 7 ≥0, х + а ≥ 0;
{х ≥ -7, х ≥ -а.
Рассмотрим 2 случая:
1) если а = 7, то имеем уравнение: √(х + 7) = х + 7. Обе части возведем в квадрат:
Х + 7 = (х + 7)²; (х + 7)(х+6)=0;;
откуда х1 = -7, х2 = -6.
2) если х + 7 > 0 (х > -7, а > 7). Решения найдем, предварительно возведя обе части в квадрат:
(√(х+а) )² = (х + 7)²;
х + а = х² + 14х + 49;
х² + 13х + 49 - а = 0.
Уравнение - квадратное. Ищем дискриминант:
D = 13² - 4(49 - a) = 169 - 196 + 4a = 4a - 27.
Вновь рассматриваем три случая:
1) 4a - 27 < 0; 4a < 27; a < 6,75 - при таких значениях параметра корней нет.
2) 4а - 27 = 0; а = 6,75 - при таком значении параметра корень единственный и он равен х = -13/2 = -6,5.
3) 4а - 27 > 0 (а > 6,75). Тогда имеем два корня:
Х1 = (-13 + √(4а - 27))/2 = -6,5 + √(а - 6,75).
Х2 = (-13 -√(4а - 27) = -6,5 - √(а - 6,75).
Объединяем все полученные нами результаты и записываем ответ.
ОТВЕТ: если а < 6,75, то корней нет; если а = 7, то х1 = -7, х2 = -6; если а = 6,75, то х = -6,5; если а є (6,75; 7)∪(7; + ∞), то х1 = -6,5 + √(а - 6,75), х2 = -6,5 - √(а - 6,75).