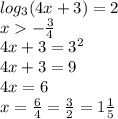
ответ: x=1.5
Объяснение: Превращаем двойку в логарифм с основанием 3
log3(4x+3)=log3 9
Так как у логарифмов одинаковые основания их можно убрать
4x+3=9
4x=6
x=1.5
Надеюсь все понятно, если что спрашивай
Для решения можно воспользоваться формулой n -го члена геометрической прогрессии. То, что лайки увеличиваются в разы, говорит о том, что они увеличиваются в геометрической прогрессии.
b₁ = 5 Лайки в первый день
q=5 (знаменатель геометрической прогрессии) Лайки увеличиваются в 5 раз ежедневно
Найти: b₁₀ Количество лайков на 10-й день
Формула нахождения n - го члена геометрической прогрессии:
b(n)=b₁ * qⁿ⁻¹
b₁₀=b₁*q¹⁸⁻¹
b₁₀=5*5⁹=5¹⁰
b₁₀=9765625
ответ: 9765625 лайков будет на 10-й день