1. 2)
2. 3)
Объяснение:
1. 
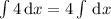, интеграл 
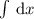табличный и равняется 
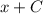, тогда исходный равняется 
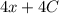, произведение констант — тоже константа, поэтому решением будет 
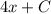, что соответствует второму варианту ответа.
2. Область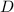 
, ограниченная указанными кривыми 
, 
, 
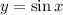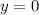и 
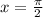, показана на приложенном рисунке. Получается, что 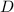задают два неравенства, 
и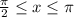 
. Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.
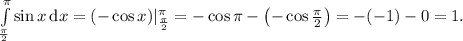
(Так получается, ибо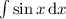 
— табличный интеграл, равный 
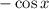, а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть 
, при известном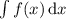 
, то есть 
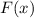, притом константа в таком случае игнорируется.)
Полученный результат соответствует третьему варианту ответа.
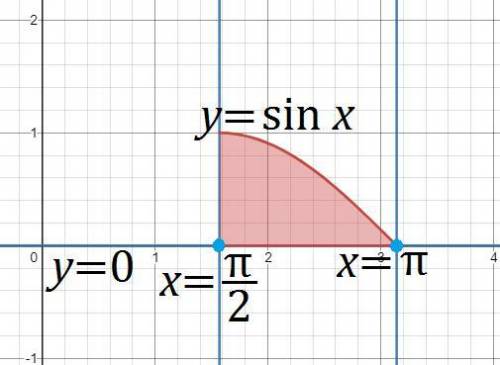
ответ: x = -π/4 + πn; x = 3π/4 - arcsin(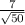
) + πn, n ∈ Z
Объяснение:
0,5sin(2x) + 7cos^2(x) - 3,5 + 3,5 = 3
0,5sin(2x) + 3,5cos(2x) = -0,5
sin(2x) + 7cos(2x) = -1
Разделим обе части на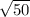
Получаем:
Пусть sin(α) =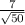
, тогда cos(α) =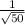 
α = arcsin(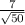
)
Получаем уравнение sin(2x)*cos(α) + sin(α)*cos(2x) = -cos(α)
Применяем формулы синуса суммы и формулу приведения
sin(2x + α) = -sin(π/2 - α)
sin(2x + α) = sin(α - π/2)
1) 2x + α = α - π/2 + 2πn
x = -π/4 + πn, n ∈ Z
2) 2x + α = π + π/2 - α + 2πn
x = 3π/4 - α + πn
x = 3π/4 - arcsin(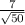
) + πn, n ∈ Z