У треугольника вершины три. Значит, в любом случае, на одной из прямых будут лежать две вершины. Очевидно, что тогда все треугольники разделятся на два класса, те у которых две вершины на первой прямой, и те, у которых - на второй. Выбрать две точки из 12 можно числом сочетаний. На каждые такие точки приходится 13 возможных третьих вершин.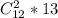 
. (Аналогично для другой прямой) 
- треугольников.
Четырехугольник имеет четыре вершины, потому имеет смысл рассматривать один их класс (ведь на каждой прямой может быть только две вершины (ибо у четырехугольника три вершины не могут лежать на одной прямой)) Выбрать первые две можно так: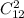 
, каждой такой паре соответствует 
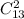пар вершин на второй стороне. тогда прямоугольников 
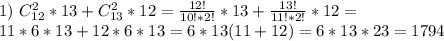
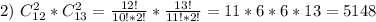
Квадрат любого выражения неотрицателен, поэтому для того, чтобы сумма двух квадратов была равна нулю, каждый из квадратов должен быть равен нулю.
Второе слагаемое несложно, из него просто получаем y=-1.
Со первых квадратом несколько сложнее:
|x-2|+|x+2|-4=0
|x-2|+|x+2|=4
Проще всего понять, что решение этого уравнения - отрезок [-2,2], можно, вспомнив геометрический смысл модуля. |x-a| - расстояние между точкой с координатой x и точкой с координатой а.
Итак, нужно найти все точки, сумма расстояний до точек 2 и -2 равна 4. Но расстояние от -2 до 2 как раз равно 4, поэтому (тут лучше нарисовать рисунок) подходят все точки отрезка, заключенного между этими двумя точками.
Обобщая все вышенаписанное, уравнение задает отрезок, соединяющий точки (-2,-1) и (2,-1).