Question

3x^2+2x+1< 0
решить неравенство
написать подробное решение ​

Answer 1

ответ: $x \in (-\infty; -\frac{1}{3}) \cup (1; +\infty).$

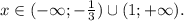
Объяснение:

-3x² + 2x +1 < 0;

3x² - 2x - 1 > 0;

Дискриминант равен 2²+4*1*3 = 4+12 = 16.

Корни трехчлена равны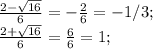 $\frac{2-\sqrt{16}}{6} = -\frac{2}{6} = -1/3;\\ \frac{2+\sqrt{16}}{6} = \frac{6}{6} = 1;$

Значит 3x² - 2x - 1 = (3x+1)(x-1) > 0;

Рассмотрим значение выражения на каждом из интервалов: (-∞; -1/3); (-1/3; 1); (1; +∞). На первом из них 3х+1 < 0 и х-1 < 0. Значит произведение больше 0. На втором 3х+1 > 0 и х-1 < 0. Значит их произведение меньше 0. На третьем 3х+1 > 0 и х-1 > 0. Значит их произведение больше 0. Подходит только интервал (-∞; -1/3) и (1; +∞)

Answer 2

ответ: найдём ецли функции. Дискриминант 4+12=16. Корни х1=(-2+4)/(-6)=-1/3, х2=(-2-4)/(-6)=1. Так как парабола имеет в маесималтной точке вершину, то искомая область от минус бесконечности до х1=-1/3 и от х2=1 до плюс бесконечности.

Объяснение: