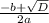 =
= 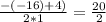 = 10
= 10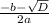 =
= 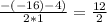 = 6
= 6Основания логарифмов равны 0,2<0, поэтому знак неравенства при переходе на сравнение аргументов будем менять на противоположный. Писать основание не буду, т.к. это неудобно здесь.
log(x-2)+logx>log(2x-3) ОДЗ: х-2>0, х>0, 2х-3>0 ⇒ х>2
log x(x-2) > log(2x-3)
x(x-2)<2x-3
x²-2x-2x+3<0, x²-4x+3<0, (x-1)(x-3)<0
Метод интервалов (1)(3). Знаки на интервалах +, -, +.
1<х<3
Учитывая ОДЗ, получаем ответ 2<х<3
8sin^2x+cos3x+1=0
4cos^3x-3cosx+8-8cos^2x+1=0
cosx=t
4t^3-8t^2-3t+9=0
t=-1
cosx=-1
x=П(2k+1)
Объяснение: