То есть существует неприводимый над Q элемент, равный 7, удовлетворяющий критерию Эйзенштейна для f(x+1). Значит f(x+1) неприводим над Q. Тогда и f(x) неприводим над Q.
Сумма внутренних углов выпуклого многоугольника равна 180(n-2), где n- число сторон в многоугольнике.Возьмем любой многоугольник и поставим внутри его точку О. Затем эту точку О соединим со всеми вершинами многоугольника. Получится n треугольников, где n - число сторон многоугольника. Сумма углов в треугольнике равна 180 градусов. А сумма углов в n треугольниках будет равна 180n. А сумма углоа вокруг точки О равна 360 градусов. И если мы из 180n вычтем сумму углов вокруг точки О, то получится 180n - 360 = 180(n-2).
Если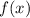 приводим над
приводим над 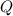 , то
, то 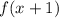 также приводим над
также приводим над 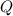
(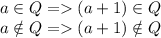 )
)
То есть существует неприводимый над Q элемент, равный 7, удовлетворяющий критерию Эйзенштейна для f(x+1). Значит f(x+1) неприводим над Q. Тогда и f(x) неприводим над Q.
Доказано.