Объяснение:
1) А(-π/2 ; -1).
Здесь х= - π/2;
Для определения принадлежит ли точка А графику функции y=cos x
подставим значение х= - π/2, в формулу данной ф-ции:
y=cos x = cos (-π/2) =0. Итак при х= -π/2 , значение ф-ции у=0, а
это значит что точка А(-π/2;-1) не принадлежит графику функции
y=cos x.
2) B(9π/4; √2/2).
Объяснение аналогично варианту 1).
x= 9π/4;
Подставляем значения х в формулу данной функции:
y=cos x= cos(9π/4) = cos(2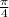
) =cos(π/4 + 2π)= cos(π/4)= √2/2;
При х =9π/4, значение функции у=√2/2, то точка В(9π/4; √2/2)
принадлежит графику функции y=cos x.
3) C(-4π;-1).
x=-4π; y=cos x= cos(-4π)=cos(-2π-2π)=cos(-2π)=cos(2π)=1;
При х= -4π, у=1.
Точка В(-4π;-1) не принадлежит графику функции y=cos x.
√(3x - 1) + √(6x² - 5x + 1) = 0
слева стоит сумма двух квадратных корней, которые всегда неотрицательны
чтобы их сумма равнялась 0 надо, чтобы каждый равнялся 0
√(3x - 1) = 0
√(6x² - 5x + 1) = 0
решаем первое x = 1/3
если при подставлении во второе то равняется 0, то корень 1/3? если нет то корней нет
6*(1/3)² - 5*1/3 + 1 = 6*1/9 - 5/3 + 3/3 = 2/3 - 5/3 + 3/3 = 0
да корень x = 1/3
√(x + 3) + √(y + 4) = 0
слева стоит сумма двух квадратных корней, которые всегда неотрицательны
чтобы их сумма равнялась 0 надо, чтобы каждый равнялся 0
√(x + 3) = 0
√(y + 4) = 0
x + 3 = 0 x = -3
y + 4 = 0 y = -4
(√(3x + 5) - 3)² = 9
если x² = a (a>0) x=+- √a
1. √(3x + 5) - 3 = 3
√(3x + 5) = 6
3x + 5 = 36
3x = 31
x = 31/3
2. √(3x + 5) - 3 = -3
√(3x + 5) = 0
3x + 5 = 0
x = -5/3
ответ -5/3 и 31/3