ответ: во вложении Объяснение:

ответ: x1=π/4+k*π, где k∈Z; x2=1/2*(-1)^(n)*arcsin(0,6)+π*n/2, где n∈Z.
Объяснение:
Перепишем уравнение в виде 2*cos²(x)+2*sin(2*x)-3=0. Так как 2*cos²(x)=1+cos(2*x), то данное уравнение можно записать в виде: 1+cos(2*x)+2*sin(2*x)-3=0, или 2*sin(2*x)+cos(2*x)-2=0. Положим 2*x=t, тогда данное уравнение перепишется в виде: 2*sin(t)+cos(t)-2=0. А так как cos(t)=√[1-sin²(t)], то его можно записать и так: √[1-sin²(t)]=2-2*sin(t), или √[1-sin²(t)]=2*[1-sin(t)]. Возводя обе части в квадрат и приводя подобные члены, приходим к уравнению 5*sin²(t)-8*sin(t)+3=0. Полагая u=sin(t), получаем квадратное уравнение 5*u²-8*u+3=0. Оно имеет корни u1=1 и u2=0,6. Если u1=sin(t1)=1, то t1=π/2+2*k*π, где k∈Z. Тогда x1=t1/2=π/4+k*π, где k∈Z. Если же u1=sin(t2)=0,6, то t2=(-1)^(n)*arcsin(0,6)+π*n, где n∈Z. Тогда x2=t2/2=1/2*(-1)^(n)*arcsin(0,6)+π*n/2, где n∈Z.
ответ: 4132 .
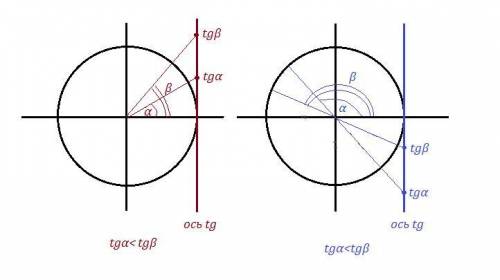
Угловой коэффициент прямой k - это тангенс угла наклона ( tgα ) прямой к положительному направлению оси ОХ.
Все острые углы α имеют положительный tgα>0 , а тупые углы - отрицательный tgα<0 .
Прямые 1 и 4 наклонены под острым углом, значит их угловые коэффициенты положительны ( k₁>0 , k₄>0 ) . А прямые 2 и 3 наклонены под тупым углом к оси ОХ , значит их угловые коэффициенты отрицательны ( k₂<0 , k₃<0 ) .
Все положительные числа больше отрицательных . Теперь сравним между собой k₁ и k₄ , а также k₂ и k₃ .
Чем больше острый угол, тем больше tg этого угла , значит k₄>k₁ .
Чем меньше тупой угол, тем меньше tg этого угла, значит k₃>k₂ .
Окончательно получаем: k₄>k₁>k₃>k₂ .
a) x = 2^5; x = 32
б) x + 5 = 4^2
x + 5 = 16
x = 11
в) log3 x = log3 2^3 + 4log3^2 5
log3 x = log3 2^3 + 4 * 1/2 * log3 5
log3 x = log3 2^3 + 2log3 5
log3 x = log3 2^3 + log3 5^2
log3 x = log3 ( 2^3 * 5^2)
log3 x = log3 ( 8 * 25)
log3 x = log3 200
x =200
г) нет решения.
N4:
а) x > 2^3; x > 8
б) x + 7 < (1/2)^-3
x + 7 < 2^3
x + 7 < 8
x < 1
N5:
5^-2+3x = 5^2
- 2 + 3x = 2
3x = 4
x = 4/3